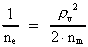|
By Louis Nielsen, Senior Physics MasterIntroductionIn the following I shall show that a connection exists between the energy states of a hydrogen atom and the total content of energy of the Universe. It will be shown that the mechanical energy of an electron in a certain state is equal to a definite fraction of the total energy of the Universe. It will be shown that the discontinuous properties are a consequence of the quantization of space, time and mass. In 1913 Niels Bohr showed (Niels Bohr (1885-1962): 'On the Constitution
of Atoms and Molecules', Philosophical Magazine, vol. 26, p. 1 (1913)),
how it was possible to quantize the energy of a H-atom, and thus give a
quantitative "explanation" of the experimental data concerning
the line spectra of the H-atom. To quantize the energy possibilities in
an H-atom, Bohr assumed ad hoc that the angular momentum of the electron,
viz. the product of its mass, velocity and distance from the proton, was
equal to a natural number multiplied by Planck's Constant divided
by 2* However, the physical quantity we call the angular momentum is
calculated by the fundamental physical quantities, distance, time and
mass, which is also the case for all other physical quantities! As a
consequence it is reasonable to assume that the quantization is already
present at this fundamental level! I shall show that the quantization
at a "higher" level is a consequence of the quantization of space,
time and mass.Fundamentally we have: (1) 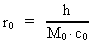 where h is Planck's Constant, c0 is the velocity of light, and M0 is the total matter/energy mass of the Universe. The time quantum – elementary time t0 is given by: (2) 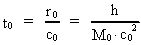
The mass of an "elementary" particle is assumed to be a fraction
of the total mass of the Universe. Every finite physical distance
(3) 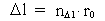
Likewise every physical time interval (4) 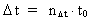 All physical quantities, such as velocity, acceleration, force, work, energy etc., are defined as usual, but we must now take into consideration the quantization of space, time and mass. This fundamental 'atomization' implies that all movement is discontinuous, all movements take place in 'jumps'. Furthermore all physical processes in a definite system will characteristically consist of discontinuous changes of certain physical quantities. Processes in a physical system can be described by the change of certain quantum numbers, belonging to definite physical quantities. All physical quantities can be expressed by the cosmically fundamental quantities: the space quantum, the time quantum and the total mass of the Universe.
Velocity and acceleration in the discontinuous movementWe define the velocity v of a particle in a definite reference system in the usual way:(5) 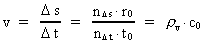
where (6) 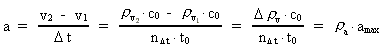
In this definition equation, we shall call
The quantum energy of the hydrogen atom.In the following I shall show that the mechanical energy, viz. the sum of the kinetic energy and the potential energy, of an electron, being in a certain state of movement in the hydrogen atom, is quantized, and that this quantum energy can furthermore be expressed by a certain fraction of the total energy of the Universe. We shall make the calculations on the following idealized model of the hydrogen atom: we shall presume that the electron moves in a closed 'quantum circle' around a proton, which we shall presume is at rest in a chosen reference system. We shall presume that the H-atom does not interact with other partial systems, which of course is impossible in the real Universe. In a first approximation we shall disregard magnetic forces, caused by the movement of the electron in its orbit and own rotation (spin) of the electron and the proton. Furthermore we shall assume that both the electron and the proton are mathematical points, which of course is not realistic. However, this mathematical idealization has proved fruitful in other contexsts, f.i. in the ideal gas model, in which it is also assumed that the particles have no extension. To make the model a little more physical, we can presume that both the proton and the electron have an extension equal to elementary length. Coulomb's electrostatic force law, which we shall use, is valid for charges of mathematical points.
The quantum energy of the electron(7) 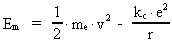 where me is the mass of the electron at rest, v its discontinuous velocity in a certain 'quantum orbit', kc is the Coulomb Constant, e the electric elementary quantum, and r the average 'quantum radius'. In order that the electron shall be able to move in a closed orbit, it must be influenced by a 'centripetal force', towards the proton. Thus we can write Newton's 2nd Law for the movement of the electron as: (8) 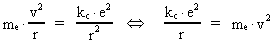 The right side of equation (8) is the expression for the electric Coulomb force. By means of equation (8) we can transform equation (7) as: (9) 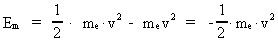 Inserting the quantized velocity expression from equation (5) we get: (10) 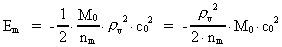 where the mass me of the electron is expressed as a whole fraction of M0, the total mass of the Universe, thus: (11) 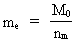
where we shall call nm the mass quantum number. (12) 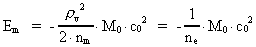
where we can call ne the electron's cosmic energy quantum
number
As the light constant c0 is equal to the ratio between elementary
length and elementary time, we see the following from equation (12):
The quantum energy of the atom is determined by elementary length,
elementary time and the total energy of the Universe. To this comes a
quantum number, dependent of the used system. In equation (12) ne
is the cosmic energy quantum number of the atom.
As the total mass in the Universe is around 1.6 ·
1060 kg (see my quantum cosmology),
which is an extremely high figure, the cosmic energy quantum number is
also extremely high, in the order of 1095. Practical calculations
with such high figures are difficult, and we can therefore for practical
reasons again introduce the rest mass of an electron in equation (12).
Quantum Physical deduction of the Rydberg Formula.In my treatise: Rational Quantum Physics, I have made a quantum physical
treatment of the empirically found
Rydberg Formula. (13) 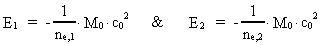 The ratio between these two energies is: (14) 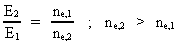 where ne,1/ne,2 gives the ratio between the electron's cosmic energy quantum numbers in the two states. This is furthermore given by: (15) 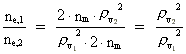
i.e. the square of the ratio between the two rational velocity quantum
numbers, corresponding to the electron's two velocities. (16) 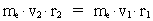 Expressing velocities and distances by quantized quantities, we get: (17) 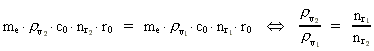
where (18) 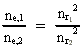 Using this in equation (14) we get a connection between the quantum energies and the space quantum numbers. We can thus write: (19) 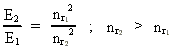 As the lowest energy state of the atom, E1, corresponds to a space quantum number nr1 = 1, we can write equation (19) as follows: (20) 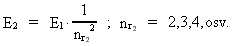 where we get the higher energy states by giving nr2 the values 2, 3, 4, etc. It should be denoted that these energies are negative, which can be seen from equation (13), and which corresponds to the bound states of the electron. If an electron goes from f.i. a higher energy state E2 to the lower state E1, the difference in energy will be emitted as a photon. As these two energy states correspond to the space quantum numbers nr1 = 1 and nr2 = 2, we can write: (21) 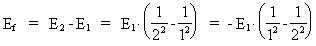
where Ef gives the energy of the emitted photon. Equation (21)
thus only expresses the demand for conservation of energy. We can now write equation (21) in a general way, corresponding to the space quantum numbers nr1 and nr2. We get (22) 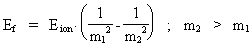 In equation (22), Eion is the measured ionization energy for a real atom. The energy of an emitted photon can now be calculated by giving the natural numbers m1 and m2 the values: m1 = 1, 2, etc. and m2 = m1 + 1. Equation (22) is formally identical to the formulas found by Balmer and Rydberg on a purely empiric base. They were not able to give a reason based on the fundamental physical condition of our Universe. It should be noted that the previous deductions are based on 'point charges', and this result in not realistic geometrical conditions. In a more realistic model, it is necessary to take into account the extension of the particles, which will give another mathematical expression of the Coulomb energy. Likewise the magnetic energy conditions due to the electron's and the proton's motions in orbit and their own motions (spin) must be considered. If these energy amounts are inserted in the calculations, it will be possible to describe the hydrogen atom's so-called fine structure and hyper fine structure. Finally I shall again underline that the previous calculations show, that the quantum aspects in our Universe are caused by the fundamental quantization of space, time and mass, and that this quantization is determined by the total and definite mass of our Universe.
2nd January 1997 Louis Nielsen.E-mail: LNi@Herlufsholm.dk Louis Nielsen, Herlufsholm.
Next article
|
 . By means of this ad hoc
supposition, Bohr could deduct a quantized energy formula, i.e. the
electron can only have quite definite and separate values of its energy.
. By means of this ad hoc
supposition, Bohr could deduct a quantized energy formula, i.e. the
electron can only have quite definite and separate values of its energy.
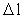 is a natural number – the
space quantum number
is a natural number – the
space quantum number 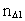 multiplied by
elementary length.
multiplied by
elementary length.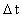 is equal to a natural number – the time quantum number
is equal to a natural number – the time quantum number
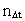 multiplied by elementary time
t0. Thus the following is valid:
multiplied by elementary time
t0. Thus the following is valid:
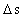 is the distance travelled
in the time interval
is the distance travelled
in the time interval 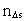 is the space
quantum number belonging to the distance
is the space
quantum number belonging to the distance 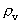 . This velocity quantum number is
from the interval between 0 and 1, as no velocity surpasses c0.
. This velocity quantum number is
from the interval between 0 and 1, as no velocity surpasses c0.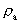 the acceleration quantum number which is seen to be a
rational number, lying in the interval 0 to 1. The ratio between the
velocity of light and elementary time c0/t0 gives
a theoretical upper limit for the acceleration of a particle. This upper
limit is denoted by amax.
the acceleration quantum number which is seen to be a
rational number, lying in the interval 0 to 1. The ratio between the
velocity of light and elementary time c0/t0 gives
a theoretical upper limit for the acceleration of a particle. This upper
limit is denoted by amax.