|
Quantization of Space, Time and Mass By Louis Nielsen, Senior Physics Master. Introduction.In the following I shall submit a theoretical description of our Quantum Physical Universe, a description in which all physical quantities are quantized. My theory is not in accordance with the current quantum mechanical description, which a.o. is based on Erwin Schrödinger's continuous wave equation from 1926. (Erwin Schrödinger (1887-1961): "Quantisierung als Eigenwertproblem", Annalen der Physik, vol. 79, p. 489, (1926), vol. 80, p. 437, (1926), vol. 81, p. 109, (1926).).Schrödinger himself was of the opinion that the wave model for quantum processes in physical systems, for which the wave equation is an expression, is only a mathematical emergency solution, lacking a better understandable quantum physical theory. In the following I shall show how it is possible to give a more understandable, and thereby a rational description of the quantum physical processes of the Universe. The theory is holistic, as it shows that the most fundamental physical quantity is the total matter/energy mass of our Universe! As it will be shown, the content of energy in every local quantum is a fraction of the total energy of the Universe. Each quantum is characterized by definite quantum numbers, and each physical process is characterized by changes in the quantum numbers. For these quantum numbers, certain upper and lower limits exist, and furthermore, certain laws of conservation are valid. My theory is based on the assumption that the fundamental physical quantities,
space, time and mass, are quantized. My discovery of this quantization and its relation
to Planck's Constant, the velocity of light and the total matter/energy mass of the
Universe is also fundamental for my Holistic Quantum Cosmology with Decreasing Gravity.
My general method in calculations within rational quantum physics is quite simple. All physical quantities are defined, based on the fundamental physical quantities: distance, time interval and mass. As a consequence of their quantization, all other physical quantities will be quantized. Quantization of physical space, i.e. a region in which 'something', in the form of 'matter' and 'fields' exist, means that we can not in our universe maintain a continuous Euclid geometry. Physically a smallest measure of length exists, the elementary length. All 'geometrical' relations shall be measured by means of this elementary quantum length. As a consequence this seems to mean that geometrical bodies in microcosmos are 'edged'. Something in our macroscopic world supports this, think about the geometrical shapes of crystals. Even the 'smoothest' surface will appear grainy, and 'edged' when magnified. Apparently we live in an 'edged' quantum universe! In the following I shall show, by simple calculations, how much energy was maximally at disposal when our Universe was created. I shall show that the energy content of a system can be calculated as the system's equivalent mass multiplied by the velocity of light to the second power. Einstein showed this, but my calculation is simpler. I shall also submit a conversion of the so-called Rydberg formula for the hydrogen atom, showing that it can be transformed to an expression in which discontinuous quantum masses appear. Physical Quantum Geometry and Rational Physical Quantum Mechanics.As a consequence of the quantization of physical space we can not maintain the continuous Euclid geometry in our description of physical phenomena. In the physical quantum geometry, for instance the Euclid/Pythagoric equations for the sides of a right angle triangle will not be exact. Neither can we retain that pi, the ratio between the circumference and the diameter of a circle, is irrational. In the physical quantum geometry we must introduce 'quantum triangles' and 'quantum circles'. Finding that the physical space quantum, called elementary length, in our daily practical units (eg meter), is an extremely small number, we can not daily observe the consequences of quantization of space and time. In the microphysical description of the world, this quantization, however, will be significantly relevant. This is also true when we want to describe and understand the earliest phases of our Universe. Generally a cosmic physical quantization prevail. The physical smallest distance in our universe - elementary length - is given by
the fractional relation between Planck's constant and the product of the total
matter/energy mass of the universe and the velocity of light in vacuum. (1) 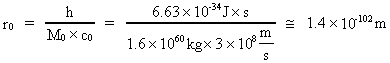
The values of Planck's Constant and the velocity of light are measured in laboratories. The value of the total matter/energy mass I have calculated by a formula, deducted in my quantum cosmological theory. The smallest physical time interval in our universe - elementary time - is given by the ratio between elementary length and the light constant. (2) 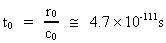
Elementary time is the smallest quantum of time in our Universe. Elementary length and elementary time define an absolute space interval and an absolute time interval. This should be understood in the way, that any observers, independent of their relative movements will 'measure' the same value of elementary length and elementary time. This can be seen from the equations, as all will measure the same velocity of light, the same matter/energy of the universe and the same Planck Constant. In other words, elementary length and elementary time are invariant in a relativistic
Lorentz transformation. As something new within the special relativity theory, elementary
length, elementary time and the total matter/energy mass of the Universe are the lower
and upper limits for the values of transformed lengths, time intervals and masses! These
limits allow us very interestingly to deduce the Compton length of a specific mass.
Furthermore, the quantization of space and time require that the relativistic Lorentz
transformations are quantized, too, being thus transformation equations between space
and time quantum numbers. The following equations are valid: (3) 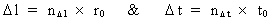
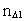 is the space quantum number and is the space quantum number and
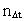 the time quantum number. the time quantum number.Both numbers are positive, natural numbers, which may only take the values 1, 2, 3, 4, ... etc.
The Quantum Circle and the Rational PI.In the physical quantum geometry a 'circle' will be quantized, eg. the 'quantum circle'
will be a polygon, where the lengths of the sides are all equal to elementary length. (4) 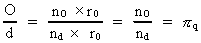
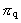
In daily practical calculations it is of no importance whether pi is rational or irrational, as we anyway round our figures to a certain numbers of significant decimals. In physical theoretical analyses, however, it is relevant to know that space is quantized. Quantum Kinematics and Quantum Dynamics. Discontinuous Movement Physics.A consequence of the space-time quantization is, that the velocity and acceleration of a particle will be quantized, too. Likewise will other physical quantities, deducted from the fundamental physical quantities - distance, time and mass - also be quantized. It should be noted that a particle here means a physical particle, i.e. a 'fluctuating' ball - a quantum ball - with an average extension equal to elementary length multiplied by a natural number. Inside this quantum ball a certain amount of energy can be stored, corresponding to the particle having a definite 'mattermass'. That the ball is 'fluctuating' or 'blurred' means that we physically seen only are
able to measure a physical quantity with a certain smallest certainty, corresponding
to Heisenberg's uncertainty relations. (5) 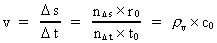
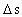 is the distance moved by the particle
within the time is the distance moved by the particle
within the time 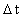 as measured by a time
measurement device, 'standard' for the used reference system. In the equation, as measured by a time
measurement device, 'standard' for the used reference system. In the equation,
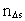 is the space quantum number and is the space quantum number and
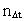 is the time quantum number. The ratio between these
two defines a rational velocity quantum number between 0 and 1.
This number is denoted
by is the time quantum number. The ratio between these
two defines a rational velocity quantum number between 0 and 1.
This number is denoted
by 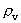
If a particle is influenced by a force, i.e. a physical influence able to give the particle a change in velocity, i.e. an acceleration, we shall define this acceleration as follows: (6) 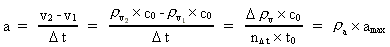
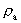 the acceleration quantum number which is seen to be a rational number,
also lying in the interval 0 to 1. The ratio between the velocity of light and
elementary time c0/t0 gives a physical upper limit for
the acceleration of a particle. This upper limit is denoted as amax
the acceleration quantum number which is seen to be a rational number,
also lying in the interval 0 to 1. The ratio between the velocity of light and
elementary time c0/t0 gives a physical upper limit for
the acceleration of a particle. This upper limit is denoted as amax
We can now develop a quantum dynamics, defining the mechanical physical quantities in the same way as in the classical newtonian mechanics.
Definition of Quantum Force.We shall define a physical force as 'something' being able to give a particle an
acceleration, measured in relation to a specific reference system. (7) 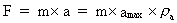
Definition of Work and Energy Transfer by a Force.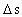 by
a constant force with the magnitude F this force has carried out a work on the particle. by
a constant force with the magnitude F this force has carried out a work on the particle.
The size 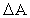 of this work we shall define by the
following expression: of this work we shall define by the
following expression:
(8) 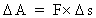
According to the definitions of the conceptions work and energy, a work carried out on a particle means that the particle has either received a certain amount of energy - the work is then positive - or has lost energy - the work is then negative. Furthermore we shall decide: A system which in some way (possibly for us a still unknown way) is able to perform a positive work, is said to contain energy. And, to repeat: Performing a work means transfer of energy from one system to another. The Total Energy of the Universe and its Present Distribution.From equations (7) and (8) we can calculate the total amount of energy of our universe, which was created or released when the universe performed its first quantum jump, about 11 billion years ago. Formally we get: (9) 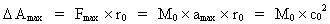
Very interestingly this is the same equation deducted by Albert Einstein in his special theory of relativity in 1905, the famous formula defining energy and mass as equivalent quantities - two sides of the same basical physical quantity. As the universe during its development has been split up in smaller and smaller matter/energy quanta, it follows immediately that a certain 'mass' must correspond to a content of energy, calculated according to the following equation: (10) 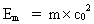
In my holistic quantum cosmology I have deducted the following quantum cosmological equation: (11) 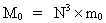
Multiplying both sides of equation (11) by c0² we get: (12) 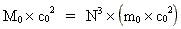
Holistic Quantum Description of the Line Spectrum of the Hydrogen Atom.The Quantum Energy of a Photon.In the year 1900 the German phycisist Max Planck (1858-1947) [Ref.: Max Planck:
"Über das Gesetz der Energieverteilung im Normalspektrum", Annalen der
Physik, vol. 4, p. 553, (1901)] was 'forced' to quantize the electromagnetic radiation
energy emitted by a so called 'black body'. This was the only possible way by which he
could explain the experimental data. Max Planck realized - but much against his will -
that electromagnetic radiation energy is quantized in 'lumps' of energy, called photons. (13) 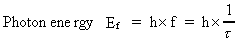
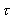 the equivalent period time. the equivalent period time.
In the classical description of electromagnetic radiation, this is considered to be a continuous phenomenon, with possibility for radiation at all possible frequencies. No upper limits have ever been set! In the here submitted holistic quantum physics, it can all be described more rational, and with the total energy of the universe as a very fundamental factor. We can rewrite equation (13) in the following way: (14) 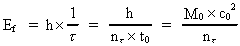
 a natural time quantum number. We can thus conclude: The energy centent of
a photon is a whole fraction of the total energy of the Universe! a natural time quantum number. We can thus conclude: The energy centent of
a photon is a whole fraction of the total energy of the Universe!
The Rydberg Formula for the Hydrogen Atom, Converted to a Universal Quantum Law.For the purpose of making a system for the wavelengths, experimentally found for the line spectrum of the hydrogen atom, the Swiss mathematician Johan Jakob Balmer (1825-1898) in 1885 'constructed' the so called Balmer Formula. This was in 1890 generalized by the Swedish physician Janne Rydberg (1854-1919). The Rydberg Formula can be written as follows: (15) 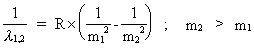
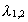 is the wavelength of a certain
spectral line, m1 and m2 are natural numbers, where m2
> m1 and R is the Rydberg Constant, which has the measured value of
R = 1.097 · 107 meter-1 is the wavelength of a certain
spectral line, m1 and m2 are natural numbers, where m2
> m1 and R is the Rydberg Constant, which has the measured value of
R = 1.097 · 107 meter-1
As the Danish physician Niels Bohr (1885-1962) showed in 1913, the right side of the
Rydberg Formula is connected with quantum processes in the photon emitting atom. Niels
Bohr could theoretically deduct the value of the Rydberg Constant by means of the
measured values of Planck's Constant, the mass and electric charge of the electron, and
the velocity of light. (16) 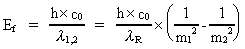
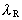 giving a length which we could call the Rydberg
Length. This physical length is equal to a natural number nR multiplied by
the elementary length r0 giving a length which we could call the Rydberg
Length. This physical length is equal to a natural number nR multiplied by
the elementary length r0
(17) 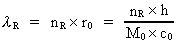
(18) 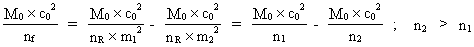
From equation (18) we see the following: all members of the equation are whole fractions of the total energy of the Universe. If we divide both sides of the equation by c0², all members are total fractions of the mass of the Universe. We can therefore also write the equation by means of masses: (19) 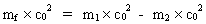
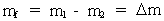
As it will be seen, the Rydberg Formula and its transscriptions only express the energy conservation law! In this section we started with the Rydberg Formula, which specifically is only valid for the radiation emission of a hydrogen atom. The transformed formula (19), however, is presumably generally valid, as it is an expression of a universal law - the conservation of energy. The equation with quantum numbers can be written as follows: (21)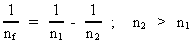
|
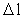 is given as a natural
number multiplied by elementary length r0. Every finite time
is given as a natural
number multiplied by elementary length r0. Every finite time



