En fotons bevægelse i et
gravitostatisk felt
anderledes analyseret end i Einsteins gravitationsteori
Af lektor cand.scient. Louis Nielsen, Herlufsholm,
Danmark
Indledning
I det følgende vil jeg vise, at man ved hjælp af den newtonske
mekanik og kvantefysiske formler, der gælder for en foton, kan komme
frem til formler, der stemmer overens med formler, der udledes i Einsteins
generelle relativitetsteori. Vi vil betragte bevægelsen af en foton
i et gravitostatisk felt. Vi finder, at både fotonens hastighed og
den til fotonen hørende »dualistiske« bølgelængde
afhænger af gravitationsfeltet.
Fotonbevægelse i et gravitostatisk felt
Vi betragter en kuglesymmetrisk aktiv gravitationel masse m, der i afstanden
r fra centrum skaber et 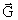 -felt givet ved: -felt givet ved:
(1) 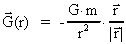
hvor G er Newtons gravitationskonstant. Fotonens bevægelsesligning er
givet ved Newtons 2. lov:
(2) 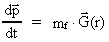
hvor  er fotonens
tidslige impulstilvækst, og mf er dens gravitationelle masse,
der ifølge Einsteins ækvivalensprincip er lig dens inertielle
masse. er fotonens
tidslige impulstilvækst, og mf er dens gravitationelle masse,
der ifølge Einsteins ækvivalensprincip er lig dens inertielle
masse.
Partikelstørrelserne 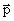 og mf vil vi udtrykke ved den til fotonen hørende
dualistiske bølgelængde.
og mf vil vi udtrykke ved den til fotonen hørende
dualistiske bølgelængde.
Lad os benytte sprogbrugen et feltfrit vacuum; hermed menes et
område af rummet, hvor der absolut ikke forekommer nogen form for
felter og ej heller stof. Hvis vi tænker os en foton i et sådant
feltfrit vacuum, da vil dens fart i forhold til et givet referencesystem
være lig med den karakteristiske konstant c0, der bl.a.
indgår i den specielle relativitetsteoris formler. Hvis en foton
befinder sig i et felt, vil den næppe have hastigheden c0,
men en derfra forskellig hastighed c.
En foton, der bevæger sig i feltfrit vacuum, vil have en total energi
E0 givet ved:
(3) 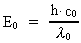
hvor h er Plancks konstant og 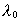 fotonens bølgelængde. Bevæger fotonen sig ind i eksempelvis
et gravitationsfelt, da vil den have en energi E, der kan skrives:
fotonens bølgelængde. Bevæger fotonen sig ind i eksempelvis
et gravitationsfelt, da vil den have en energi E, der kan skrives:
(4) 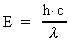
hvor c er hastigheden i feltet og
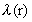 dens
bølgelængde i feltet. dens
bølgelængde i feltet.
Idet vi antager, at fotonens energi under bevægelsen er konstant,
får vi:
(5) 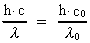
dvs. at forholdet mellem fotonens hastighed og bølgelængde er
konstant, hvorimod de hver for sig kan variere. Da 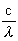 angiver frekvensen, ses denne at være
konstant. angiver frekvensen, ses denne at være
konstant.
Fotonens inertielle masse og dermed gravitationelle masse kan fås fra
Einsteins energi-masse-relation:
(6) 
Da 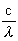 er konstant,
ser vi, at fotonen opretholder en konstant masse, selv om dens hastighed
ændrer sig. Dette gælder ikke for »stoflige« partikler,
idet deres inertielle masse vokser med hastigheden. er konstant,
ser vi, at fotonen opretholder en konstant masse, selv om dens hastighed
ændrer sig. Dette gælder ikke for »stoflige« partikler,
idet deres inertielle masse vokser med hastigheden.
Fotonens impuls p er givet ved:
(7) 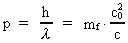
Ved benyttelse af (6) og (7) kan vi opskrive fotonens bevægelsesligning
således i et 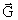 -felt, idet vi betragter
en radial bevægelse: -felt, idet vi betragter
en radial bevægelse:
(8) 
Idet 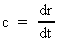 kan (8) omskrives til: kan (8) omskrives til:
(9) 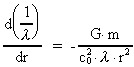
hvor udtrykket i ligning (1) er indsat.
Ved separation af de variable 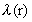 og r
fås: og r
fås:
(10) 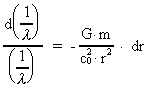
Ligning (10) kan integreres til:
(11) 
hvor a < r1 < r2 er afstandene til to punkter
regnet fra centrum af den graviterende masse m, der antages kuglesymmetrisk
med en radius a. 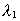 og og
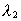 er fotonens bølgelængder
svarende til r1 og r2. er fotonens bølgelængder
svarende til r1 og r2.
Lader vi r2 gå mod »uendelig« svarende til et
feltfrit område, hvor bølgelængden er 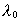 , så kan vi skrive: , så kan vi skrive:
(12) 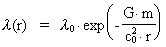
hvor 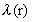 er bølgelængden
svarende til afstanden r. er bølgelængden
svarende til afstanden r.
Da 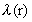 og c er ligefrem proportionale,
gælder følgende ligning for fotonhastigheden c(r) i en afstand
r fra den graviterende masse: og c er ligefrem proportionale,
gælder følgende ligning for fotonhastigheden c(r) i en afstand
r fra den graviterende masse:
(13) 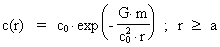
Hvis 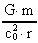 er væsentligt mindre
end 1, hvilket opfyldes af de fleste objekter, da kan vi med en rimelig
nøjagtighed rækkeudvikle til første orden. Vi får
da følgende udtryk for er væsentligt mindre
end 1, hvilket opfyldes af de fleste objekter, da kan vi med en rimelig
nøjagtighed rækkeudvikle til første orden. Vi får
da følgende udtryk for 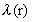 og
c(r) : og
c(r) :
(14) 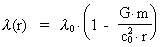
(15) 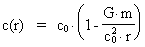
Ligning (12) viser, at en foton, der bevæger sig i et gravitationsfelt,
»udsættes« for en bølgelængdeændring
samtidig med, at dens hastighed også ændres. En fotons hastighed
som funktion af afstanden r fra den graviterende masse m er givet ved
ligning (13).
Gravitationel bølgelængdeforskydning
Lad os beregne den relative bølgelængdeændring svarende
til to afstande r1 og r2, idet vi benytter udtrykket
i (14). Vi får:
(16) 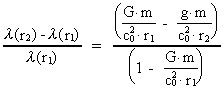
hvor 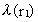 er bølgelængden i
afstanden r1 og er bølgelængden i
afstanden r1 og 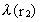 er
bølgelængden i afstanden r2. er
bølgelængden i afstanden r2.
Hvis en foton udsendes fra eksempelvis solens overflade, hvor r1
~= 7 · 108 m, og denne fotons
bølgelængde måles ved jordens overflade, hvor r2
~= 1,5 · 1011 m, da fås med en solmasse
m = 2 · 1030 kg og r2 >> r1:
(17) 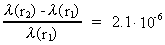
Denne talværdi stemmer pænt overens med den faktisk målte
bølgelængdeændring og svarer ganske til det resultat, man
udleder i Einsteins generelle relativitetsteori, dog med den store forskel,
at man i den sidstnævnte teori opererer med frekvensen i stedet for som her
med bølgelængden. (Se f.eks. C. Møller: The Theory of
Relativity, Oxford, 1952, p. 346).
Lyshastigheden i den generelle relativitetsteori
I den generelle relativitetsteori udledes en formel for »lysets«
hastighed i et gravitationsfelt (se f.eks. C. Møller, p. 353). Formlen er:
(18) 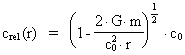
altså hvor der indgår en kvadratrod i modsætning til en
eksponentialfunktion i formel (13).
Hvis (18) rækkeudvikles til 1. orden, bliver den helt identisk med (15).
I (18) er der en kritisk afstand rs givet ved:
(19) 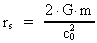
Denne afstand kaldes Schwarzschild-radius og angiver, i hvilken afstand
lyshastigheden bliver nul. Hvis r < rs, bliver
crel(r) imaginær, og dette giver ikke-fysiske forhold.
Begrebet »et sort hul« defineres som et objekt, hvis masse er
koncentreret inden for afstanden r < rs. I formel (13) er der
ingen kritiske afstande, hvilket gør den mere fysisk end formel (18).
Lysafbøjning omkring en graviterende masse
Det, der gjorde Einstein berømt, var en »tilsyneladende«
bekræftelse af et fænomen, som han havde forudsagt i sin
generelle relativitetsteori. Einstein beregnede, at en lysstråle, der
passerer tæt forbi solen, vil blive afbøjet 1,75 buesekunder.
Halvdelen af denne afbøjning var forårsaget af en ændring
af lyshastigheden beregnet efter formel (18). Den anden halvdel var bestemt
af rummets »krumning«, der var bestemt af størrelsen af den
tilstedeværende gravitationelle masse. Denne »krumning« af
rummet beregnes af Einsteins »geometriske« feltligninger.
Ved en solformørkelse i 1919 foretog Arthur Eddington en ekspedition
til et sted, hvor formørkelsen ville blive total. Under
»totaliteten« af formørkelsen fotograferede man denne og de
omkringliggende stjerner, af hvilke der kun var ganske få. Ved en
sammenligning med et fotografi af det samme stjerneområde, men uden
solen, kunne man konstatere en afbøjning. Analysen var dog meget
primitiv og med stor spredning i de målte afbøjninger.
En gravitationel afbøjning følger også af den formel (13),
som jeg har udledt, men denne giver for solens vedkommende omkring 0,87
buesekunder. En yderligere afbøjning forårsages af det
gravitationelle rotationsfelt (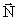 -feltet),
der er omkring alle graviterende masser, der er i relativ bevægelse.
Da solen roterer, vil dette give anledning til et -feltet),
der er omkring alle graviterende masser, der er i relativ bevægelse.
Da solen roterer, vil dette give anledning til et 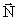 -felt,
som giver en kraftpåvirkning på enhver gravitationel masse, der
bevæger sig i feltet. -felt,
som giver en kraftpåvirkning på enhver gravitationel masse, der
bevæger sig i feltet. 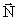 -feltet
skal beregnes af de gravitationelle feltligninger, som jeg har redegjort for
i min artikel: En Maxwell-analog gravitationsteori
med to gravitationsfelter. -feltet
skal beregnes af de gravitationelle feltligninger, som jeg har redegjort for
i min artikel: En Maxwell-analog gravitationsteori
med to gravitationsfelter.
Se evt. Hans Christophersens kronik
Næste artikel
Hovedsiden
| 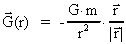
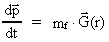
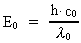
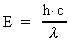
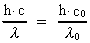

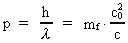

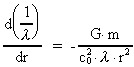
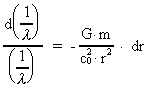

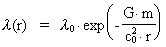
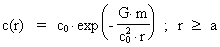
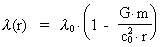
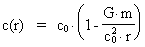
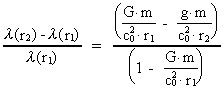
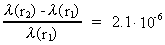
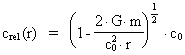
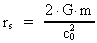
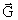 -felt givet ved:
-felt givet ved:
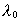 fotonens bølgelængde. Bevæger fotonen sig ind i eksempelvis
et gravitationsfelt, da vil den have en energi E, der kan skrives:
fotonens bølgelængde. Bevæger fotonen sig ind i eksempelvis
et gravitationsfelt, da vil den have en energi E, der kan skrives:
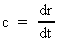 kan (8) omskrives til:
kan (8) omskrives til:
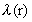 og r
fås:
og r
fås:
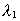 og
og
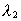 er fotonens bølgelængder
svarende til r1 og r2.
er fotonens bølgelængder
svarende til r1 og r2.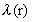 er bølgelængden
svarende til afstanden r.
er bølgelængden
svarende til afstanden r.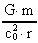 er væsentligt mindre
end 1, hvilket opfyldes af de fleste objekter, da kan vi med en rimelig
nøjagtighed rækkeudvikle til første orden. Vi får
da følgende udtryk for
er væsentligt mindre
end 1, hvilket opfyldes af de fleste objekter, da kan vi med en rimelig
nøjagtighed rækkeudvikle til første orden. Vi får
da følgende udtryk for 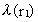 er bølgelængden i
afstanden r1 og
er bølgelængden i
afstanden r1 og 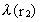 er
bølgelængden i afstanden r2.
er
bølgelængden i afstanden r2.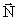 -feltet),
der er omkring alle graviterende masser, der er i relativ bevægelse.
Da solen roterer, vil dette give anledning til et
-feltet),
der er omkring alle graviterende masser, der er i relativ bevægelse.
Da solen roterer, vil dette give anledning til et