|
– elementarkvantet der opbygger stof, felter og 'vacuum' Opdagelsen af en universel kvanteæter
Af lektor cand.scient. Louis Nielsen,
Herlufsholm, Danmark
Indledning
Æteren og Michelson-Morleys forsøg
En af de forklaringer, som flere efterhånden accepterede, var en geometrisk effekt; dette selv om en sådan var ganske mærkværdig. I 1889 foreslog den irske fysiker Georg Fitzgerald (1851-1901), at hvis legemer forkortes i deres bevægelsesretning, da kunne dette give en forklaring på Michelsons forsøg. I 1892 fremsatte den hollandske fysiker Hendrik Antoon Lorentz (1853-1928) ligeledes tanken om en længdeforkortning. Lorentz (H. A. Lorentz: »Versuch einer Theorie der electrischen und optischen Erscheinungen in bewegten Körpern«, Leyden (1895)) viste, at hvis genstande – og dette gælder også målestokke – forkortes med faktoren 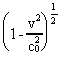 i bevægelsesretningen, da
kan dette forklare Michelsons eksperiment. I ovenstående faktorudtryk
er v en genstands hastighed i bevægelsesretningen i forhold til
æteren og c0 lysets hastighed i æteren. Lorentz
kunne give en elektromagnetisk forklaring af længdeforkortningen.
I senere teorier indførte Lorentz i øvrigt også
koordinatrelative tidsforløb, hvilket førte til
transformationsligninger mellem koordinatsystemer, der bevæger sig
jævnt i forhold til hinanden. Hvis disse transformationsligninger
benyttes på de maxwellske ligninger, vil disse vise sig at blive
invariante – dvs. have samme matematiske form – over for en
koordinattransformation. Disse transformationsligninger blev af Albert
Einstein (1879-1955) kaldt for Lorentztransformationen, idet det
viste sig, at Einstein kunne udlede de samme transformationsligninger,
som Lorentz havde opstillet, dog udledt fra tilsyneladende helt andre
grundprincipper. Disse grundprincipper er udgangspunktet for Einsteins
specielle relativitetsteori fra 1905 (A. Einstein:
Annalen der Physik, vol. 17, (1905)). Udgangspunktet er følgende
antagelser: i bevægelsesretningen, da
kan dette forklare Michelsons eksperiment. I ovenstående faktorudtryk
er v en genstands hastighed i bevægelsesretningen i forhold til
æteren og c0 lysets hastighed i æteren. Lorentz
kunne give en elektromagnetisk forklaring af længdeforkortningen.
I senere teorier indførte Lorentz i øvrigt også
koordinatrelative tidsforløb, hvilket førte til
transformationsligninger mellem koordinatsystemer, der bevæger sig
jævnt i forhold til hinanden. Hvis disse transformationsligninger
benyttes på de maxwellske ligninger, vil disse vise sig at blive
invariante – dvs. have samme matematiske form – over for en
koordinattransformation. Disse transformationsligninger blev af Albert
Einstein (1879-1955) kaldt for Lorentztransformationen, idet det
viste sig, at Einstein kunne udlede de samme transformationsligninger,
som Lorentz havde opstillet, dog udledt fra tilsyneladende helt andre
grundprincipper. Disse grundprincipper er udgangspunktet for Einsteins
specielle relativitetsteori fra 1905 (A. Einstein:
Annalen der Physik, vol. 17, (1905)). Udgangspunktet er følgende
antagelser:
En – for mange fysikere dramatisk – konsekvens af Einsteins specielle relativitetsteori var Einsteins påstand: Der eksisterer ingen universel æter! Den specielle relativitetsteori kunne redegøre for resultatet i MichelsonMorleyforsøget. Spekulationerne om en æter kunne hermed ophøre, mente tilhængerne af relativitetsteorien. At kaste en idé væk, der havde præget den naturfilosofiske tænkning siden oldtiden, var naturligvis ikke nemt.
Antallet af unitoner og deres fordeling i universet (1) 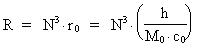 hvor R er universets aktuelle udstrækning, N = 4,16 · 1042 er forholdet mellem de elektrostatiske og gravitostatiske kræfter mellem en elektron og en positron. r0 er universets elementarlængde, der bestemmer forholdet mellem Plancks konstant og universets samlede energi-/stofmasse M0 multipliceret med lyskonstanten c0. Ligning (1) kan omskrives til følgende sammenhæng: (2) 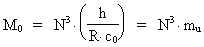
I ligning (2) angiver mu den fysisk mindste masse i det aktuelle
univers, en masse jeg har kaldt elementarmassen. Da denne masse svarer til
et diskret kvantum af energi, betegnes dette energikvantum som en uniton. (3) 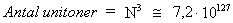
altså et uhyre stort antal.
At geometrisk fordeling, tæthed og bevægelsesforhold er bestemmende for stoffers egenskaber, er vi ganske bekendt med. Som et eksempel kan jeg nævne følgende tre stoffer: Grafit, diamant og carbon-60-molekylet. De består alle af carbon-atomer; den væsentligste forskel er den geometriske opbygning. Som bekendt har disse forskellige carbonstrukturer vidt forskellige egenskaber! På analog måde kan alt være opbygget af unitoner! Da 'stof' på et højere niveau består af elektroner, protoner og neutroner, kan vi beregne, hvor mange unitoner der er 'bundet' i 'stofpartiklerne', hvis vi kender antallet af 'stofpartikler' i hele universet. Jeg vil antage, at der er omkring N² 'stofpartikler' i universet. Dette antal er omkring 106 gange større end det såkaldte 'Eddingtontal', der skulle angive antallet af protoner og elektroner i universet. Dette 'Eddingtontal' blev udregnet af den engelske astrofysiker Arthur Eddington (1882-1944). (A. S. Eddington: The Mathematical Theory of Relativity, Cambridge, (1923)). Jeg vil antage, at det 'bundne stof' i universet er ækvivalent med N² elektroner. Antallet af unitoner, der opbygger én elektron er givet ved: (4) 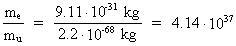
hvor me er elektronens masse, og mu er unitonens masse.
Vi ser, at en elektron består af et uhyre stort antal unitoner! Mange spørgsmål kan stilles:
Vi kan beregne det gennemsnitlige rumfang, som en uniton har til rådighed. Af ligning (1) kan vi beregne universets nuværende totale rumfang, idet vi antager kugleform: (5) 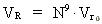 VR er rumfanget af universet med en udstrækning R, og Vr0 er rumfanget af en kugle med en udstrækning lig med elementarlængden r0. Rådighedsrumfanget for en uniton Vu er da givet ved: (6) 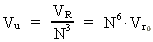 Den gennemsnitlige udstrækning ru af rådighedsrumfanget for en uniton er: (7) 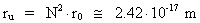 Den beregnede talværdi af ru er af størrelsesorden lig med udstrækningen af en elektron! Den gennemsnitlige unitonmassedensitet i universet er bestemt af: (8) 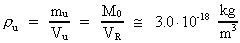 Af ligningerne (1) og (7) får vi for forholdet mellem universets udstrækning R og en 'fri' unitons rådighedsstrækning ru: (9) 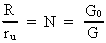 Vi ser, at forholdet er lig med forholdet mellem de elektrostatiske og gravitostatiske kræfter mellem en elektron og en positron, eller lig med forholdet mellem gravitations-»konstantens« størrelse, da universet blev 'født', og den nuværende gravitations-»konstant«. Massen Ms af de unitoner, der er 'bundet' i stof, antager jeg givet ved følgende udtryk: (10)
hvor me er elektronens masse.
Analogi mellem lydudbredelse og lysudbredelse gennem
unitonrummet
(11) I ligning (11) angiver v bølgens udbredelsesfart (fasehastigheden). Den generelle løsningsfunktion til differentialligningen (11) er givet ved: (12) hvor f1(x-v·t) angiver en bølge, der udbreder sig i den positive x-akses retning, og f2(x+v·t) en bølge, der bevæger sig i modsat retning. Løsningen (12) angiver således en superpositionsløsning. Bølger, der udbreder sig i rummet, tilfredsstiller den mere generelle differentialligning: (13) 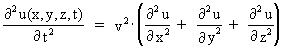 hvor y og z er retninger vinkelret på x-aksen. Udbredelsesfarten af en given bølge er bestemt af bølgemediets fysiske egenskaber, eksempelvis om der er tale om et gasformigt, flydende eller fast stof. For en gas, hvor bølgeudbredelsen foregår adiabatisk, dvs. hvor der ikke sker varmeudveksling mellem vekselvirkende 'volumenelementer', gælder følgende formel for udbredelseshastigheden, v: (14) 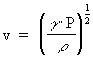
hvor Hvis der er tale om en ideal gas, dvs. et idealiseret partikelsystem, hvor der ikke virker kræfter mellem partiklerne, så kan man benytte følgende tilstandsligning: (15)
hvor P er gastrykket, Den absolutte temperatur Ta af en gas er defineret som værende ligefrem proportional med den gennemsnitlige kinetiske energi af en enkelt partikel. Hvis den enkelte partikel har tre bevægelsesfrihedsgrader, da defineres følgende: (16)
hvor <v²> er den kvadratiske middelværdi af de enkelte
partiklers hastigheder. (17) Da unitonen er det mindste kvant i universet, er det rimeligt at påstå, at den inden for sit rådighedsrum bevæger sig med en gennemsnitlig hastighed lig med c0, der er den største hastighed i universet. Idet det antages, at lys er svingningsudbredelse gennem unitonrummet, og vi antager, at formlerne, der gælder for udbredelse af partikelsvingninger, også er gældende for unitonerne, får vi for udbredelseshastigheden v af unitonsvingningerne, dvs. lysvirkningerne: (18) 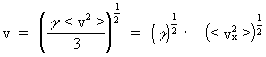
idet der gælder, at: <vx²> = 1/3 ·
<v²>, der angiver udbredelseshastigheden langs en x-akse.
For (19) altså en udbredelseshastighed gennem unitonmediet, der svarer til lyshastigheden. Lysudbredelse fra sted til sted kan således tænkes at være udbredelse af unitonsvingninger. Et nærmere kendskab til unitonernes bevægelsesforhold og vekselvirkninger vil kunne give bedre indsigt. Af ligning (16) kan vi bestemme unitonrummets ækvivalente absolutte temperatur Ta med en unitonmasse m1 = 2.2 · 10-68 kg og <v²> = c0²: (20) 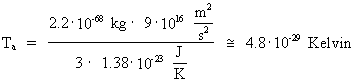 Vi ser, at unitonrummets temperatur er yderst tæt på det absolutte temperaturnulpunkt. Ved så lav en temperatur må unitonmediet have superflydende egenskaber; bl.a. må det være friktionsfrit. Denne friktionsløshed bevirker, at alle „makroskopiske” legemer kan bevæge sig friktionsfrit gennem unitonrummet. Unitoner og deres hastigheder I min holistiske kvantekosmologi vises det, at universet i vor epoke indeholder omkring 10127 stof-/energi-kvanter. Disse er dannet ved kvantedesintegration af den oprindelige kosmiske embryoton – det urkvant som hele vort univers er dannet af. Jeg har givet disse elementarkvanter navnet unitoner. Den nuværende masse mu af en uniton er i vor epoke omkring 2.2·10-68 kg. Den gennemsnitlige fordeling af unitonerne i universet svarer til en gennemsnitlig rådighedsafstand mellem unitonerne af en størrelsesorden på omkring 10-17 m. Se afsnittet om unitonen. Et vigtigt spørgsmål er: Hvilke hastigheder kan unitoner bevæge sig med? Den umiddelbare fysiske logik siger os, at unitonen som det mindste ’stofkvant’ i universet må bevæge sig med den største hastighed i universet. Med vor nuværende viden menes denne hastighed at være lyshastigheden i det, man kalder vacuum. Om der eksisterer overlyshastigheder er et omstridt spørgsmål. Flere forskergrupper har dog udført forsøg, der tyder på muligheden af overlyshastigheder. I det følgende vil jeg vise, at en uniton bevæger sig med minimum (?) lyshastigheden c0. Denne påstand kan jeg formelmæssigt begrunde på følgende måde: Lad os benytte Louis Victor de Broglies (1892-1987) formel: (Louis de Broglie, Comptes Rendus, vol.177, (1923)) (21)
hvor Vi stiller spørgsmålet: Hvilken minimumshastighed
vmin har en uniton svarende til den største fysiske
’bølgelængde’? Den største fysiske afstand er universets
aktuelle udstrækning R. Den største fysiske ’bølgelængde’
må være lig med R, dvs., (22) idet
© Louis Nielsen
Unitonstød som fysisk-mekanisk forklaring af gravitation og inerti Af lektor, cand. scient. Louis Nielsen, Herlufsholm Siden Isaac Newton (1642-1727) i 1660'erne opdagede den matematiske
lovmæssighed for gravitationskræfterne mellem to kuglesymmetriske legemer,
har fysikere søgt efter en fysisk-mekanisk årsagsforklaring til
gravitationsvirkningerne. Newton selv opstillede ingen hypoteser, der kunne give
en fysisk forklaring af gravitationen, men at gravitationsvirkningerne skulle
kunne udbrede sig i et absolut tomt rum og med en uendelig stor hastighed,
accepterede Newton ikke. Dette fremgår bl.a. af en brevveksling, som Newton
havde ved årskiftet 1692-93 med Richard Bentley (1662-1742), der var kapellan
i London. I sit tredje brev til Bentley skriver Newton (Isaac Newton's Papers and
Letters on Natural Philosophy, ed. I. B. Cohen, Cambridge, Havard University Press,
1958):
Ideerne om en universel 'æter' blev afskaffet, da Albert Einstein (1879-1955)
fremkom med sin specielle relativitetsteori i 1905. (Annalen der Physik, vol. 17,
(1905)). Einstein mente ikke, at der var behov for eksistensen af et universelt
'transportmedium' for hverken lys eller gravitation. I 1915 fremkom Einstein med
sin generelle relativitetsteori, der også skulle give en 'forklaring' af
gravitationsfænomenerne. Einstein forklarer gravitation som en geometrisk
rum-tids effekt, der er bestemt af tilstedeværelsen af stof/energi.
Kort formuleret er indholdet i Einsteins gravitationsteori:
Selv om et universelt medium ikke er en konsekvens af Einsteins gravitationsteori,
kunne Einstein dog ikke afvise eksistensen af et sådant.
I min 'Holistiske kvantekosmologi med aftagende gravitation'
(se denne), er det en naturlig konsekvens, at der eksisterer en universel
'kvanteæter' bestående af uhyre små elementarkvanter, som jeg
kalder unitoner (se afsnittet om Unitonen). Unitonerne bevæger sig med
minimum lyshastigheden. Da disse unitoner kan vises at være til stede i
hele universet, også i det man kalder vacuum kan det meget vel være
disse elementarkvanter, der ved stødvirkninger er den fysiske årsag
til de gravitationelle virkninger, ja endog elektriske kræfter, andre
kraftvirkninger og legemers inertivirkninger.
I dag accepterer de allerfleste fysikere Einsteins gravitationsteori uden at
have et dybere kendskab til denne. Man har lært det i skolen og på
universitetet, så det skal nok passe, siger man, og det stiller man sig
tilfreds med uden at tvivle.
I næste afsnit vil jeg kort omtale en mekanisk-fysisk teori for gravitation,
som blev udviklet i slutningen af 1700-tallet.
George-Louis Le Sages mekaniske gravitationsteori
I slutningen af 1700-tallet fremsatte den schweiziske matematiker og fysiker
George-Louis Le Sage (13/6-1724–9/11-1803) en mekanisk gravitationsteori.
(George-Louis Le Sage, 'Lucréce Newtonien', Memoires de l'Académie
Royale des Science et Belles-Lettres de Berlin. Berlin 1784). Teorien er
behandlet af bl.a. Pierre Prevost (Pierre Prevost , 'Traité de Physique
Méchanique de Georges-Louis Le Sage.' Deux Traités de Physique
Méchanique. Geneva, 1818). Teorien er baseret på følgende
hypoteser:
I et appendix til 'Lucréce Newtonien' opsummerede Le Sage, hvilke
egenskaber de 'ultramundane corpuskler' måtte have. Følgende
måtte gælde:
Størrelsen af de kræfter, der skubber legemerne sammen,
kan vises at være ligefrem proportional med produktet af legemernes masser
og omvendt proportional med afstandens kvadrat, hvilket er identisk med Newtons
gravitationslov! At størrelsen af de kræfter, der skubber legemerne
sammen, er ligefrem proportional med legemernes masser, kræver, at de
stofpartikler, som et givet legeme består af, er diskret fordelt, og at
der er meget tomrum mellem partiklerne.
Le Sage's teori havde både tilhængere og modstandere. Modstanden
skyldtes, at Le Sages teori byggede på flere til dels uafhængige hypoteser.
Teorien var ikke en logisk konsekvens af en mere grundlæggende fysisk teori.
Eksempelvis var den kinetiske molekylteori og den temodynamiske teori endnu ikke
udviklet, og dette betød, at Le Sages teori nærmest gik i glemsel i
de næste hundrede år, efter at den var opstillet. Med den kinetiske
molekylteoris udvikling i slutningen af 1800 tallet blev Le Sages teori taget op
til fornyet analyse af så gode fysikere som James Clerk Maxwell (1831-1879)
(James Clerk Maxwell, 'Atom', Encyclopaedia Britannica, ninth edition, vol. 3, 1890)
og William Thomson (Lord Kelvin) (1824-1907) (William Thomson, 'On the ultramundane
corpuscles of Le Sage', The London Edinburgh and Dublin Philosophical Magazine
and Journal of Science. Vol XLV, London 1873). Fysiske indvendinger mod Le Sages
teori var bl.a. følgende: Hvis planeterne bevæger sig gennem et
partikelfyldt rum, da vil dette bevirke, dels at planeterne vil blive bremset,
dels at deres temperatur vil stige. Friktionsproblemet kan fjernes, hvis de
'utramundane korpuskler' er uhyre små og bevæger sig med hastigheder,
der er meget større end de makroskopiske legemers hastigheder.
Opvarmningsproblemet blev foreslået løst af Kelvin, idet han som i
den kinetiske molekylteori opererede med tre kinetiske energimuligheder, nemlig
translatorisk, rotatorisk og oscillatorisk. Når en 'gravitationspartikel'
overfører impuls til et legeme og derved får en nedsættelse i
f.eks. den translatorisk kinetiske energi, kan dette energitab kompenseres ved
en evt. delvis forøgelse i den rotatoriske og/eller oscillatoriske energi.
Georg Howard Darwin (1845-1912) (søn af Charles Darwin (1809-82) og
professor i astronomi ved Cambridge Universitet) viste, at Le Sages 'ultramundane
korpuskler' måtte foretage uelastiske kollisioner med de legemer, de
stødte imod, hvis stødkræfterne skal kunne reproducere
Newtons gravitationslov. (Georg H. Darwin, 'The Analogy between Le Sage's
Theory of Gravitation and the Repulsion of Light'., Proceedings of the Royal Society,
vol. 76, (1905)).
Det kosmiske unitonfelt som kraftformidler Et af problemerne med Le Sages gravitationsteori var, at den ikke var
en konsekvens af en mere fundamental fysisk teori. Da den kinetiske molekylteori
og termodynamikken var udviklet, kunne disse teorier danne grundlag for den
mekaniske del af teorien. Tilbage stod dog den helt afgørende antagelse,
nemlig at hele universet skulle være 'fyldt' af de 'ultramundane korpuskler'.
Denne antagelse var en ad hoc-antagelse, der ikke var en konsekvens af
eksempelvis en kosmologisk teori.
I min 'Holistiske kvantekosmologi med aftagende gravitation'
er det en konsekvens af teorien, at hele universet er 'fyldt' med de til enhver tid
mindste fysiske stof/energikvanter, — elementarkvanter, som jeg kalder UNITONER.
Som det fremgår af min kvantekosmologiske teori, startede hele universet
med ét kvant som jeg kalder for den kosmiske embryoton (den kosmiske
fosterpartikel). Udviklingen af universet 'styres' af et kosmisk
evolutionskvantetal (-det kosmiske kvanteur-) der 'tikker' op igennem de
naturlige tal! Universet blev 'født', da det kosmiske
evolutionskvantetal antog værdien 1! I vor epoke er dette kosmiske
evolutionskvantetal nået op til det uhyre store tal omkring
7 · 10127.
For hvert 'tik' af det kosmiske evolutionskvantetal opstår et nyt
stof/energikvant – en ny uniton! Antallet af unitoner er på ethvert
stadium af universets udvikling lig med den aktuelle talværdi af det
kosmiske evolutionskvantetal N³. I vor epoke er antallet af unitoner uhyre
stort. På grund af universets udvidelse sker der en forminskelse af
unitontætheden i universet samtidig med, at unitonmassen bliver mindre og
mindre — dette fordi jeg i min teori antager, at den samlede masse af
universet er konstant. Denne udtynding af det kosmiske unitonfelt kan give en
fysisk-mekanisk forklaring på, hvorfor gravitationen i vort univers er
stadigt aftagende!!
Unitoner har en uhyre lille udstrækning og bevæger sig med
lysets hastighed (muligvis med endnu større hastighed). Alt 'stof'
antages at bestå af unitoner. Således forestilles en elektron at
være et 'sammenskubbet' dynamisk system af omkr. 1037 unitoner.
At en elektron er et unitondynamisk system betyder, at den i en
ligevægtstilstand emitterer og absorberer lige mange unitoner pr. tidsenhed.
Da unitonerne kan være de 'partikler', der forårsager
gravitationskræfterne – og for den sags skyld også andre kendte
kræfter, og da disse elementarkvanter tilsyneladende opfylder de
kriterier, som Le Sages gravitationsteori kræver, kan der være god
grund til at tage denne mekaniske teori op til fornyet studium her 200 år
efter, at den blev fremsat af den fysisk-mekanisk intuitive fysiker og matematiker
George-Louis Le Sage.
For uddybning, se også: Unitonmekanisk forklaring af
gravitationskræfter.
Louis Nielsen, 20. okt. 1997
|
 : luft), som man havde indført allerede i oldtiden som
det såkaldte 5. element (i oldtiden var æteren 'det himmelske
element'; de fire andre var jord, vand, luft og ild). Dette ætermedium,
der var fordelt over hele universet, mente alle fysikere havde reel
eksistens, selv om man ikke vidste, hvad det bestod af.
: luft), som man havde indført allerede i oldtiden som
det såkaldte 5. element (i oldtiden var æteren 'det himmelske
element'; de fire andre var jord, vand, luft og ild). Dette ætermedium,
der var fordelt over hele universet, mente alle fysikere havde reel
eksistens, selv om man ikke vidste, hvad det bestod af.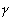 er forholdet mellem gassens
specifikke varmekapacitet ved konstant tryk og ved konstant volumen.
P er gassens tryk, og
er forholdet mellem gassens
specifikke varmekapacitet ved konstant tryk og ved konstant volumen.
P er gassens tryk, og 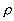 er gassens
massedensitet.
er gassens
massedensitet. 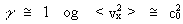 fås:
fås: