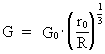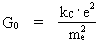In the following I shall show that what we call 'inertia' and 'gravitation' is intimately connected and that this is a consequence of my 'Holistic quantum cosmology' (see this). A result of this is that 'everywhere' in the Universe there exist some physically smallest discrete energy/matter quanta, which I call unitons. The existence of a ubiquitous 'cosmic uniton sea', consisting of unitons moving in all directions at extremely high speeds, can give a mechanical explanation of both gravitational and inertial forces. Somewhere else I shall show that the temperature of the cosmic uniton sea in our epoch is very near to absolute zero. What we call 'matter' is 'condensations of unitons' in the extremely cold cosmic uniton sea and can be considered as Bose-Einstein condensations! As an example, an electron is a uniton dynamical subsystem interacting with the cosmic uniton field. Electric forces can, therefore, also be referred to as interactions between unitons. See 'New Cosmological Model of the Electron.'

If 'the quantity of mass' of a given portion of 'matter' is defined as being proportional to the number of unitons, by which this 'portion' consists, then this will give a uniton mechanical explanation why the so called inertial mass is equal to the so called gravitational mass, and thereby why inertial forces and gravitational forces are equivalent. My claim is that both inertial and gravitational forces are caused by mechanical interaction between the unitons, of which a given body consists, and the unitons in the cosmic sea of unitons. Such connection is in agreement with the so called 'Mach's Principle'.

The geometrical extension of one uniton correspond to the physically smallest 'distance measuring unit'. This I have named a spaton. A uniton 'possesses' the actually smallest amount of energy and thereby the smallest magnitude of force. I shall define 'time', based on changes in a naturally given system. With a steady growing number of unitons in the Universe this can give us a meaningful and secure definition of the quantity we can choose to denote as 'cosmic time'. That the quantized cosmic time, corresponding to the actual age of the Universe, goes only in one direction, called 'the arrow of time', can be explained by the fact that the number of unitons in the Universe is constantly increasing. In the following the 'quantized cosmic time' is defined as being proportional to the actual number of unitons in the Universe.

If the total cosmic entropy is being defined to be proportional to the number of unitons in the Universe, this can explain why the entropy of the Universe is still increasing.

The cosmo-holistic formula. The cosmic uniton field and the decreasing uniton mass

The basis for my holistic quantum cosmology and holistic quantum physics is the following cosmo-holistic formula, uniting the microphysical and macrophysical constants:

(1)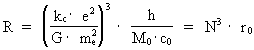

In equation (1) R is the actual extension of the Universe, k_C is Coulomb's constant, e the electric charge of the electron, m_e the gravitational mass of the electron and G the actual value of Newton's gravitational 'constant', which in my theory is a discretely decreasing quantity. N is the value of the actual ratio between the electrostatic and the gravitostatic forces between two electrons. N³ appears as a discrete cosmic evolution quantum number, 'ticking' up through the natural numbers. When the Universe was 'born' N³ took on the number one.

r₀ is the physically smallest distance in the Universe, elementary length and has connection to Planck's constant h, velocity of light c₀ in so called vacuum and the total energy/matter of the Universe, M₀ by the following equation:

(2)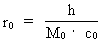

Equation (1) expresses that the actual extension of the Universe is determined by a natural space quantum number multiplied by the elementary length, which is given by equation (2).My discovery is that the cosmic space quantum number is equal to N³ .

M₀ which I call the total energy/mass of the Universe, gives an upper limit to the inertial and gravitational effects and also determines the maximum available energy of the Universe. M₀ is a very fundamental quantity and is, together with elementary length and elementary time, the physical basis for my holistic quantum cosmology. Basically: each physical distance is equal to a natural number, the space quantum number, multiplied by elementary length, each physical time interval is equal to a natural number, the time quantum number, multiplied by elementary time. Each mass is furthermore a whole fraction of the total mass of the Universe, or a natural number, the mass quantum number, multiplied by elementary mass.

As mentioned N is the actual ratio between the electrostatic and the gravitostatic forces between two electrons, but N can also be considered as the ratio between the gravitational 'constant', G₀ when the Universe was born, and the actual value of G in a definitive quantum state of the Universe. For increasing R, which means an expanding Universe, G decreases. From equation (1) we get:

(3)

where

From equation (1) we also get:

(4)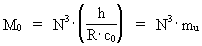

In equation (4) m_u is a physically smallest value of mass, the quantum mass. This must mean the existence of a smallest energy/matter quantum in the Universe. This smallest energy/matter quantum I have given the name UNITON. We see that m_u is an invariant, absolute and cosmological mass unit, which I have called a 'masson'. When the Universe is developed in cosmic quantum jumps - and R thereby increases - the number of unitons grows whereby the cosmic mass unit will decrease. From equation (4) we see that the actual number of unitons in the Universe is equal to the actual value of the cosmic evolution quantum number, N³.

In our epoch N³ = 7.2 · 10¹²⁷

We see that the mass of an uniton is inverse proportional to the actual number of unitons in the Universe.

The average density of unitons n_u,cos, viz. the number of unitons per volume unit, in the Universe is, except for a geometrical factor, approximately given by:

(5)

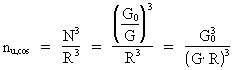With an extension of the Universe of R = 10²⁶ m we get in our epoch that n_{u,cos ,} is of the order 7 · 10⁴⁹ unitons per m³

From equation (5) we see, that the uniton density of the Universe is decreasing (if the Universe expands!), even if the number of unitons is still growing.

From equation (1) we get for the increase D (N³) of unitons:

(6)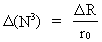

where D R is a quantized increase of the extension of the Universe. For every cosmic quantum jump, corresponding to D R = r₀, one new uniton is created. It must be assumed that the new unitons are created on the border between the existing Universe and a new coming greater Universe. A certain fraction - probably corresponding to N² electrons - of the unitons in the Universe, is Bose-Einstein condensed in what we call 'matter and which at a higher level appear as electrons, protons and neutrons.

From equations (1) and (4) can be deducted an equation, showing how the mass of an uniton decreases as the Universe expands.

Let us consider two quantum states of the Universe, which is characterized by the extension R₁ = n₁·r₀ and an extension R₂ = n₂·r₀ , where n₂>n₁ are two cosmic evolution quantum numbers. The corresponding uniton masses are denoted m_u,₁ and m_u,₂

The following connection is valid:

(7)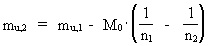

For a cosmic quantum jump we have: n₂ = n₁+1 and we can write the increase in uniton mass, D m_u , as:

(8)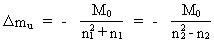

From the expression in (8) we see that the negative growth in uniton mass (corresponding to decreasing uniton mass) gets smaller and smaller as the cosmic evolution quantum number increases.

In our epoch, where the cosmic evolution quantum number has reached an extremely high value, the uniton mass decreases extremely little.

An important question: what is the physical content of equation (8)? As the mass of the uniton gets smaller and smaller as the Universe expands, this can not be explained by a simple 'matter division' of locally existing unitons.

But the decreasing mass of the unitons can be a measure of a decreasing inertial mass, and if this is the explanation it means that the inertial property of matter is not an inner property, but determined by influence of outer forces. The question then is: what is the origin of such forces trying to prevent acceleration of a body? The answer must be: the inertial effects of forces are caused by unitons in the cosmic uniton field.

Mach's principle. The cosmo-holistic principle.

Since the earlist childhood of mechanics there have been many thoughts devoted to the so called fictive forces, also known as system forces, as they appear in accelerated systems. Examples of these system forces - which are also denoted inertial forces - are: centrifugal forces and Coriolis forces. The question is: are these forces fictive, viz. 'imaginay' or are they real physical forces, caused by physical systems?

This question was especially taken up by Isaac Newton (1642-1727), George Berkeley (1685-1753), Ernst Waldfried Josef Wenzel Mach (1838-1916) og Albert Einstein (1879-1955). The problem can be considered as follows:

Consider a ball rotating in relation to the rest of the matter in the Universe. Experience shows, that the ball will bulge at the equatoreal areas. The question now is: Why does the ball bulge? Newton said: The ball bulges, because it rotates in relation to absolute space. If the ball is resting in relation to absolute space, it will not bulge, said Newton. Mach, however, said, that this relative effect would just as well appear if the whole Universe rotated in relation to the ball. Newton and Mach thus disagreed. Ernst Mach analyzed the concepts inertia and gravitation in his book 'Die Mechanik' from 1883. Einstein accepted Mach's explanation and tried to incorporate what he called 'Mach's principle' in his general theory of relativity, he did however not succeed unambiguously.

Mach's principle can be formulated as follows:

I shall formulate a totally general principle, 'The cosmo-holistic principle' :

Everything determines everything.- Omnia determinant omnia.

From equation (3) and (4) we get the following connection:

(9)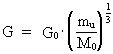

Equation (9) gives a connection between gravitation - determined by G - and the value of the uniton's mass, determined by m_u . Equation (9) also contains the total mass of the Universe, M₀ and is thus in agreement with 'Mach's principle', which 'says', that local inertial and gravitational effects are determined by the total distribution of matter in the Universe.

We see from (9), that both gravitational forces and inertial forces decrease when the Universe increases in quantum 'jumps'! Notice that the found relations are all contained in the 'cosmo-holistic formula'!

Rearranging equation (9), the uniton mass can be expressed by the decreasing gravitational quantity G:

(10)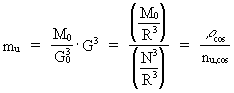

In equation (10) r_cos gives the average mass density of the Universe and n_u,_cos the average number of unitons per volume unit. We see, that what I denote as the mass of an uniton is determined by the distribution of mass and unitons in the Universe, thus in agreement with Mach's principle.

By means of the cosmic uniton sea, both gravitational and inertial forces, such as centrifugal and Coriolis forces, can be explained as caused by interactions with unitons, between the unitons of which a particle consists and the unitons in the uniton sea.

What is mass? Mass as a measure for number of unitons. The equivalence principle.

Some physical fundamental questions:

• What is mass a measure for, and how is it defined?
• Do we have an unambiguous definition?
• Is mass an inner quality of matter?
• Or is it a quantity we have introduced, lacking deeper understanding of the real conditions, and thereby for practical reasons?

The last question I shall reply with 'yes', and the two former with 'no'. In my opinion matter does not possess inner qualities corresponding to the quantities of mass defined in physics. In the established physics you operate mainly with three definitions of mass, namely: 1) The inertial mass, 2) the active, gravitational mass, and 3) the passive, gravitational mass. The three mass quantities are defined as follows:

The inertial mass of a limited system of matter - a body - is a measure of its inertia, or resistance, presented by the body when it is being accelerated, viz. gets a change in velocity, measured in relation to a given reference system. The inertial mass of a body is defined as a proportionality constant in Newton's 2nd law:

(11)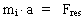

m_i is the inertial mass of the body, a is the magnitude of the acceleration caused by a resulting force of the magnitude F_res.

The active gravitational mass is defined as a measure of the magnitude of the active gravitational field existing around a given distribution of matter. The passive gravitational mass of a 'particle' (which does not disturb the active gravitation field considerably) is a measure of the magnitude of the gravitational force on the particle, when it is situated in an active gravitational field.

It is an extremely important experimental realization that the inertial mass of a portion of matter is proportional to the gravitational mass of the same portion of matter, in suitable units - f.i. kg - they have the same value. This equality between inertia and gravitation was strongly emphazised by Isaac Newton (1642-1727). Newton tested the equalities by means of swinging pendulums, where the pendulum bodies were made of different material. More accurate tests were performed at the end of 1890, by the Hungarian physicist Roland von Eötvös (1848-1919). Von Eötvös used a torsion balance which he originally had developed for measuring of local variations in gravity. Also newer and much more exact equipment has shown an identity between inertial and gravitational mass. This identity suggests an intimate connection between inertial og gravitational effects. The equality of inertial and gravitational masses is formulated in the socalled 'equivalence principle'. This principle is the basis of Einstein's general theory of relativity and can shortly be formulated :

A kinematic acceleration field is equivalent to a gravitational field, induced by matter.

According to Einstein's general theory of relativity it should be impossible by any physical experiment to show any difference between a 'kinematic gravitational field' and a 'gravitational field induced by matter'.

According to my 'Maxwell analog gravitational theory with two gravitational fields' (see this) there is a straightforward difference, seen from a field point of view, between a 'kinematic gravitational field' and a 'gravitational field induced by matter'. This difference gives an experimental possibility to separate the two cases. But when analysing the effects of forces on the fundamental uniton mechanical level, the equalities appear, as both the gravitational forces and the inertial forces are caused by uniton interactions!

Gravitational forces and inertial forces (and so far all forces) are results of interactions between unitons, and the strength of the forces are a.o. influenced by the number of interacting unitons. As the number of interacting unitons is determining the observed effects of forces between the systems, it is appropriate to have a physical quantity of mass, defined by the number of unitons. Let us therefore define the following cosmic mass quantity based on a definite number of unitons:

Likewise, a limited portion of matter (a body) shall be understood as a region with a definite number of unitons.

The hereby defined cosmic mass quantity is a cosmic invariant quantity, which in principle just requires a counting of unitons. Other intelligent creatures in the Universe will also be able to determine the cosmic mass of a portion of matter, principally, just by counting

Let us define the cosmic mass, m, of a body, by:

(12)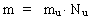

where m_u is a proportionality factor defined as the cosmic mass of one uniton and which can be chosen to have the unit kg. N_u is the number of unitons of which the body consists.

In cosmological units, where m_u is chosen as mass unit - one masson - the numerical value of m is equal to the number of unitons a body consists of. In cosmological units the mass of a body is determined by a counting of the number of unitons, and measuring mass is thus changed to a counting process!

Using (10) the mass m can be expressed by M₀, G₀ and G or by the density of mass and the density of unitons in the Universe:

(13)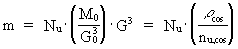

By the expression in (13) we see that the inertia of a body depends on the density of mass - and the density of unitons in the Universe. This is completely in agreement with Mach's principle. We see that this is also valid for G.

The concept of 'time' has been analysed by many thinkers, especially philosophers. However, they have not reached any agreement on an unambiguous definition of the concept. Even as 'time' plays a fundamental roll in description of physical phenomena, namely as a 'running independent variable', only very few physicists have been occupied by the fundamental 'concept of time'. As far as I see it, the problem is a matter of definition, as it is important to define any concept given by a specific word, as unambiguous as possible. A definite concept, given by a specific word, should not have different meanings, not at all if it is a concept used in nature scientific studies. If a superior concept as 'time' is given more meanings, then it should be split up in 'part concepts', each given by a specific word or a choice of more words. You can thus define and talk about 'physical time', (viz. 'natural time'), 'biological time', 'psycological time' , 'historical time' etc. Regarding 'physical time' this can advantagely be split up in: 'local physical time' and 'cosmic physical time'. To be able to compare these two measurements of time, there must exist a connection between them. The 'cosmic time measurement', which I here shall define, is an invariant and absolute quantity, whereas a defined 'local physical time' is a relative quantity.

We can ask:

• What shall we understand by 'physical time'?
• How can we define the concept 'physical time' unambiguously?
• Can an invariant and absolute cosmic time quantity be defined?

I shall define the concept of 'time' in the following way:

With an expression from latin, we can say: 'TEMPUS MUTATIO EST'

In nature, many changes occur, the question is: Which changing processes shall we choose for a definition of time? With the above knowledge of a constantly, discretely growing Universe, a cosmic physical time interval D T can be defined:

or:

(14)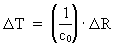

where we - for reasons of units - have chosen the reciprocal value of the velocity of light, c₀ as proportionality constant. The numerical value of the velocity of light is measured referring to a locally defined time measurement. As the smallest increase of D R = r₀ viz. equal to the physical elementary length, we see that this corresponds to a smallest time interval t₀ - elementary time given by:

(15)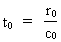

Using equation (6) we can also write (12) as:

(16)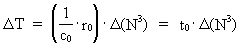

From equation (16) we see, that D T = t₀ for D (N³) = 1 , viz. one new uniton is created for every quantum time interval equal to elementary time, and corresponding to one cosmic quantum jump.

Elementary time defines an invariant and absolute cosmological time unit, which I denote a tempon . As the present Universe consists of 7.2× 10¹²⁷ unitons, viz. until our epoch this number have been formed,, this corresponds to an age of the Universe of 7.2× 10¹²⁷ tempons.

The actual age of the Universe, T, is thus direct proportional to the actual number of unitons N³. Elementary time plays the roll as a proportionality constant. We thus get:

(17)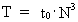

The absolute age of the Universe can thus - principally - be determined by a 'counting process'!

The connection in equation (17) gives the solution to what we call 'the arrow of time', viz. the fact that processes in the Universe always run in a definite direction. This direction is apparently the direction in which the number of unitons is increasing!

The actual extension of the Universe, R, is also determined by the number of unitons, and everything in the Universe is determined by the number of unitons! You could say: 'Count and you shall know'!.

There is the following connection between the age of the Universe and the mass of one uniton:

(18)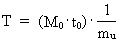

From equation (18) we see, that the actual age is inverse proportional to the actual mass of one uniton. Thus 'cosmic physical time' can be said to be equivalent to the mass of one uniton!

  Next article