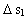|
Palæogravitationelle studier tyder på en aftagende gravitation Universets alder bestemt ved palæogeologi Af lektor, cand. scient. Louis Nielsen, Herlufsholm, Danmark
Indledning En af konsekvenserne i min holistiske kvantekosmologi er en
stadigt aftagende gravitation i universet. Da universet blev 'født',
var gravitationen omkring 1042 gange større end i vor
epoke. Inden for de første kosmiske tidsintervaller aftog
gravitationen uhyre hurtigt, og parallelt hermed opdeltes den kosmiske
embryoton – det kosmiske urkvant – i flere og flere kvanter, der
spredtes ud i et større og større universrum. Disse
'universkvanter', som jeg har givet navnet unitoner — se:
om unitoner — er de fundamentale
byggeelementer, som 'stof', 'felter' og såkaldt 'vacuum' er opbygget
af. I vor epoke er antallet af unitoner uhyre højt, omkring
7,2 · 10127. I en fysisk forklaringsteori, der skal besvare
spørgsmålet: 'Hvad er den fysiske årsag til
gravitationsvirkningerne?' kan unitonerne meget vel være de
årsagsgivende!
(1)
hvor T er universets aktuelle alder.
En tjekkisk forskergruppe under ledelse af Jindrich Hladil fra det Geologiske Institut i Prag har studeret forstenede deformationsstrukturer forårsaget af faldende sten, der har løsrevet sig fra isklumper, der har flydt på overfladen af en dyb sø. Ved en stens fald gennem vandet opnår denne efter en vis faldstrækning en konstant hastighed på grund af den opadrettede friktionskraft fra vandet og den opadrettede opdriftskraft. Summen af disse to kræfter er da lig med den nedadrettede tyngdekraft. Ved sammenstød med bundsedimentlaget borer stenen sig ned i en vis dybde, afhængig af bundlagets materialebeskaffenhed. Deformationsstrukturen vil være afhængig af den kinetiske energi, som stenen havde lige før sammenstødet med bundstoffet. De tjekkiske forskere har i laboratoriet prøvet at efterligne de geometriske og materialemæssige forhold, som var til stede for omkring 440 millioner år siden. Ved forsøg under disse simulerede forhold har det vist sig, at deformationsdybden i vandbundlaget og den geometriske deformationsstruktur er anderledes i dag, end den var i tidligere geologiske epoker. Den mest nærliggende konklusion af disse analyser er: Tyngdekraften har været større i tidligere epoker! Nærmere redegørelser kan studeres i følgende referencer:
I det følgende vil jeg foretage nogle kvantitative overvejelser vedrørende de effektforskelle, som en aftagende gravitations forårsager. Jeg vil udlede en formel, der viser, hvordan tyngdeaccelerationen ved Jordens overflade ændrer sig i tidens løb, og hermed hvilke ændringer dette giver for legemers fald i nærheden af Jordens overflade.
Variationen af tyngdeaccelerationen ved Jordens overflade Tyngdeaccelerationen g ved Jordens overflade er ifølge Newtons 2. lov og Newtons gravitationslov bestemt ved: (2)
hvor G er den aktuelle værdi af Newtons gravitations-'konstant',
der varierer med universets udvikling, mj er jordens masse og r
dens radius, der også varierer i tidens løb.
(3) En aftagende G medfører en generel afstandsforøgelse mellem graviterende masser. Jeg har tidligere vist gyldigheden af følgende ekspansionsformel: (4) Af ligningerne (3) og (4) fås følgende sammenhæng: (5) Ved brug af udtrykket i ligning (1) fås en sammenhæng mellem den relative variation af g og universets aktuelle alder T: (6) Ligning (6) kan umiddelbart integreres til: (7)
hvor indeksene 1 og 2 refererer til henholdsvis en lavere og en
højere alder af universet.
Legemers fald og sammenstødsvirkninger i forskellige geologiske epoker
Legemers bevægelsesforhold i nærheden af Jordens overflade
er bestemt af størrelsen af tyngdeaccelerationen det
pågældende sted. Hvis tyngdekraften har været
større i tidligere epoker, vil dette bl.a. bevirke, at
faldhastigheden af en genstand har været større og dermed
den kinetiske energi. Hvis en sådan genstand støder imod et
underlag, der lader sig deformere, eksempelvis sand, vil den trænge
et stykke ned i underlaget og samtidig lave et 'sammenstødskrater'
med en bestemt geometrisk form, der afhænger af materialets
beskaffenhed og den kinetiske energi, genstanden har lige før
sammenstødet. Det tryk, genstanden påvirker underlaget med,
vil også være bestemmende for kraterstrukturen.
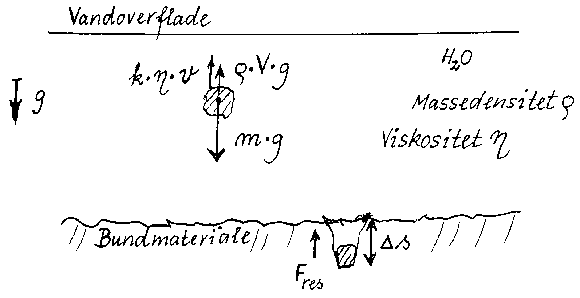
Under faldet er stenen påvirket af tre kræfter, nemlig den nedadrettede tyngdekraft Ft og de to opadrettede kræfter, henholdsvis friktionskraften Ff fra vandet og opdriftskraften F0. Størrelserne af de tre kræfter er givet ved: (8) hvor m er stenens masse og g den aktuelle tyngdeacceleration. (9)
hvor k er en geometrisk bestemt faktor, (10)
hvor (11)
Stenens maximale kinetiske energi Ek,max er givet ved: (12)
Ved nedslaget i bundmaterialet bremses stenen op over en strækning
(13) hvor c1 er en geometrisk og materialeafhængig konstant.
Den dybde (14) 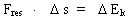
der udsiger, at den resulterende krafts arbejde er lig med tilvæksten
i en genstands kinetiske energi. Formel (14) gælder kun, hvis
Fres er konstant over strækningen
Af ligningerne (12), (13) og (14) fås for (15) 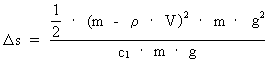 som vi dog vil skrive som: (16) hvor C er defineret ved: (17)
Af ligning (16) ser vi, at for konstant C er (18) 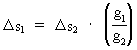 g2 og g1 kan være tyngdeaccelerationerne til to forskellige universaldre, svarende til 'i dag' og en tidligere geologisk epoke.
På steder, hvor C har samme talværdi 'i dag' som i tidligere
geologiske epoker, vil
Ved beregning af talværdierne har jeg benyttet, at universets nuværende alder T2 er omkring 10,5 · 109 år svarende til den talværdi, jeg angiver i min holistiske kvantekosmologi. En højere talværdi af T2 vil ikke ændre meget på tallene for g1 i tidligere epoker. I øvrigt kan nøjagtige palæogravitationelle studier sætte os i stand til at bestemme universets alder, et forhold, jeg vil betragte i næste afsnit.
Universets alder bestemt ved palæogravitationelle studier Da ligning (7) giver en sammenhæng mellem tyngdeaccelerationerne ved en klodes overflade – eksempelvis Jordens – til to forskellige universaldre, giver dette en mulighed for at bestemme universets alder ved palæogravitationelle analyser. Meget nøjagtige og sikre palæogravitationelle studier kan da også være med til at bekræfte min teori om en stadigt aftagende gravitation i universet. Lad os omskrive ligning (7) på følgende måde: (19)
hvor (20) 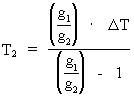
Hvis g2 er tyngdeaccelerationen ved Jordens overflade 'i dag',
og g1 og
Louis Nielsen
|
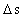 ned i bundmaterialet. Vi vil undersøge, hvordan
ned i bundmaterialet. Vi vil undersøge, hvordan
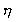 er væskens viskositetskoefficient, og v er stenens
øjeblikkelige hastighed, der antages at være relativt lav,
således at førstepotensudtrykket for gnidningskraften er
anvendeligt.
er væskens viskositetskoefficient, og v er stenens
øjeblikkelige hastighed, der antages at være relativt lav,
således at førstepotensudtrykket for gnidningskraften er
anvendeligt.
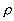 er væskens massedensitet
og V stenens volumen, svarende til det volumen væske, der
fortrænges langs stenens faldbane. Efter en vis faldvej vil summen
af Ff og F0 være lig med Ft, og
den maximale hastighed af stenen vil være opnået. Denne
maximale hastighed Vmax vil da være givet ved:
er væskens massedensitet
og V stenens volumen, svarende til det volumen væske, der
fortrænges langs stenens faldbane. Efter en vis faldvej vil summen
af Ff og F0 være lig med Ft, og
den maximale hastighed af stenen vil være opnået. Denne
maximale hastighed Vmax vil da være givet ved:
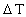 er antal millioner år
før 'i dag'
er antal millioner år
før 'i dag'