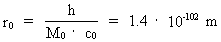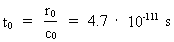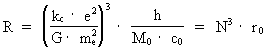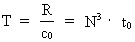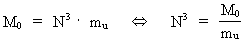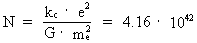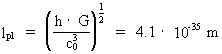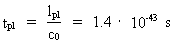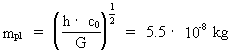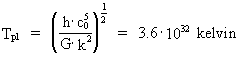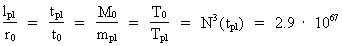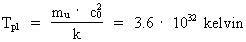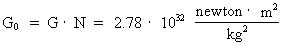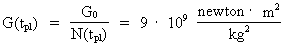|
The Cosmological Quantum Units and the Planck Units
By Louis Nielsen, Herlufsholm, Danmark
Comments are welcome to:
LNi@Herlufsholm.dk
Introduction
The socalled Planck units are not based on a physical theory, and neither
are they themselves base for a physical theory. They are 'constructed'
purely ad hoc by a dimension analysis, based on Newton's
gravitational constant, the velocity of light and Planck's constant.
The intention of Max Planck was – in 1899 – to find a unit of length, a
unit of time and a unit of temperature, independent of specific local
systems and the existence of man.
Reference: Max Planck: 'Über irreversible Strahlungsvorgänge'.
Sitzungsberichte der Preußischen Akademie der Wissenschaften, vol. 5, p. 479 (1899).
Most cosmologists, trying to describe the earliest phases of our universe
by a Big Bang model, use the Planck time unit, about 10-43 sec,
as the nearest possible time which can be used to approach the 'moment' of
Big Bang. Events before the Planck time cannot be described by the
conventional cosmological theories. Einstein's general theory of
relativity, which is basical for the accepted cosmological models,
collapses when somebody tries to analyse the early Universe. The reason
is a.o. that the theory is not based on quantum physics.
The cosmological quantum units, discovered by me, elementary length,
elementary time and elementary mass, which are basical for my
holistic quantum cosmology (see this), are as such
much more fundamental than the Planck units. In the following I shall
show the context between my quantum cosmological units and the Planck
units, and furthermore I shall show which role the Planck units play
in my holistic quantum cosmology. I shall give an explanation of the
socalled Planck mass, which is about 5.5·10-8 kg,
and the socalled Planck temperature, about 1032 kelvin.
Especially what the relatively great Planck mass concerns, it has
until now been an enigma. In the following I shall give the solution.
Elementary length, elementary time, elementary mass and the
Planck units
Basical for my holistic quantum cosmology is the existence of a smallest
physical length, elementary length r0, a smallest
physical time interval, elementary time t0 and a
smallest physical mass, elementary mass mu.
r0 and t0 are given by:
(1) 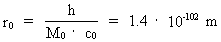
and
(2) 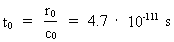
where h = 6.63·10-34 J·s is Planck's constant,
c0 = 3·108 m/s is the velocity of light, and
M0 = 1.6·1060 kg is the total matter/energy mass
of the Universe, as calculated in my holistic quantum cosmology.
The mass of the Universe is an utterly fundamental quantity, determining
both local as well as cosmological-physical states. This interaction
between local and cosmical we can call the holistic principle.
Some fundamental equations in my holistic quantum cosmology are the
following cosmological basic equations, where it should be noted that
the equations (4) and (5) are deducted from equation (3), which could be called
the holistic formula as it connects physical quantities from
microcosmos and macrocosmos:
(3) 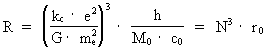
(4) 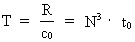
(5) 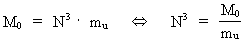
where R is the actual extension of the Universe, kc = 9 ·
109 (newton·m²)/ coulomb² is
Coulomb's constant, me = 9.11 · 10-31 kg the mass
of the electron, e = 1.6 · 10-19 coulomb its
electrical charge, G Newton's gravitational 'constant' and T the actual
age of the Universe. mu is the actual mass of the physically
smallest matter/energy quantum, elementary mass, when the extension
of the Universe is R and its cosmic age T. This physically smallest
matter/energy quantum I have given the name a uniton. N is the
ratio between the electrostatical and gravitostatical forces between two
electrons, and is given by:
(6) 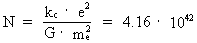
in our epoch of the evolution of the Universe.
N3 plays the role as a cosmic evolution quantum number,
which had the value 1 (one) when the Universe was 'born'. From equation (5)
we see that N3 is equal to the number of unitons in the Universe,
when the extension is R and its age is T.
When the Universe was 'born' it consisted of one quantum – the cosmic
embryoton. Gradually as the evolution quantum number was 'ticking'
up through the natural numbers, the original cosmical embryoton
disintegrates in more and more elementary quanta – unitons. In our
epoch there are about 7.2 · 10127 unitons. As I assume
that the mass of the Universe – during its whole existence – is constant,
this means that the mass of a uniton decreases gradually as the Universe
expands.
The Planck length lpl, the Planck time tpl, the
Planck mass mpl and the Planck temperature Tpl are
given by the following expressions:
(7) 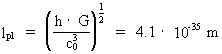
(8) 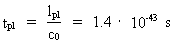
(9) 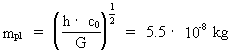
(10) 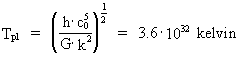
In (10), k = 1.38·10-23 J/K is Boltzmann's constant, which
is a coupling parameter between the energy of a system and its equivalent
absolute temperature.
The context between the cosmological elementary units and the
Planck units
We get a context between the Planck units and the units discovered by me
by writing the ratio between the Planck length lpl and the
elementary length r0. We get:
(11) 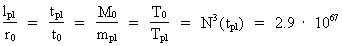
where N3(tpl) is the value of the cosmic
evolution quantum number, when the Universe had an extension equal
to the Planck length and an age equal to the Planck time. This number –
which is a natural number – also gives the number of matter/energy
quanta – unitons – in the Universe, when its age was Planck time!
T0 = 10.4 · 1099 kelvin is the formal
energy equivalent absolute 'particle temperature' when the Universe was
'born'. As the temperature value is a statistically defined quantity,
related to a system containing a great amount of particles, T0
is a purely formal quantity, as the Universe only consisted of one
quantum – the cosmic embryoton – when it was 'born'.
Comparing with the cosmological basic equation (5) we see the
following:
The Planck mass is equal to the mass of a uniton, when the
Universe had the age equal to Planck time!
When the Universe had an extension equal to the Planck length
4.0·10-35 m, with an age equal to Planck time
1.3·10-43 s,
it consisted of 2.9·1067 unitons, each with a mass equal
to the Planck mass 5.5·10-8 kg! The equivalent
absolute temperature of the Universe, Tpl, was in this state
3.6·1032 kelvin and can be calculated by:
(12) 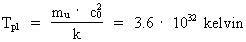
where mu = 5.5 · 10-8 kg = mpl
which is identical to the value in equation (10).
The gravitational 'constant' when the Universe had an age
equal to Planck time
From my holistic quantum cosmology it follows that gravitation in the
Universe is constantly decreasing. The context between Newton's
gravitational 'constant', G, at an age, T, of the Universe, and its
value G0, when the Universe was 'born' is given by:
(13) 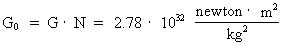
From (13) we can calculate the value of G when the Universe had an age
equal to Planck time, and we get:
(14) 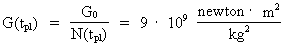
thus about 1020 times higher than in our epoch. This value
is equal to Coulomb's constant. Whether this is accidental is worth
a consideration.
From the above we see that the Planck quantities are 'just' some
connected values for physical quantities, characterizing the Universe
when it had an extension equal to the Planck length. The Planck
quantities can be deducted from the most fundamental physical
quantities in the Universe:
Elementary length, elementary time and the total matter/energy
mass of the Universe!
© Louis Nielsen, 29.november 1997
E-mail: LNi@Herlufsholm.dk
Next article
Main entry
|