Paleogravitational Studies indicate Decreasing Gravity.The age of the Universe Determined by Paleogeology.By Louis Nielsen, Senior Physics Master.Introduction.One of the consequences of my Holistic Quantum Cosmology is a continuously decreasing gravity in the Universe. When the Universe was 'born', gravity was about 1042 times greater than in our epoch. Within the first cosmic time intervals, gravity decreased extremely fast, and parallel hereto the cosmic embryoton - the cosmic archaic quantum - was split up in more and more quanta, spreading over a greater and greater universe. These 'universe quanta', which I have given the name unitons - see the section The Uniton - are the fundamental elements which 'matter', 'fields' and socalled 'vacuum' are built from. In our epoch, the number of unitons is extremely high, about 7.2 · 10127. In a physical explanation theory which shall answer the question: "What is the physical cause to gravitational effects?", the unitons may well be the answer. In our epoch gravity decreases extremely slow and it has done so during the last several billion years. In my holistic quantum cosmology I deduct the following equation for the variation of Newton's gravitational 'constant', G: (1) 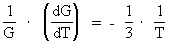 where T is the actual age of the Universe. As the decrease of gravity in our epoch is very slow it will require extremely sensitive instruments to measure it directly. Other indicators will be necessary for confirmation. By observation of distant astronomical objects - corresponding to a look back in time - gravitation dependent effects can give witness of a varying gravity. As gravity was greater in earlier epochs, this has also influenced geological conditions on the Earth. Actually the acceleration of gravity at the surface of the Earth has been greater in earlier geological epochs. Signs of a decreasing gravity can thus be discovered by studies of geological structures, dependent on gravity. In very old geological structures, which are quickly 'fossiled', and which have been untouched up to our time, it is highly probable to find signs of varying gravity. A Czech research group, headed by Jindrich Hladil from the Geological Institute in Prague, has studied fossiled deformation structures, caused by falling stones which have loosened from lumps of ice, floating on the surface of the water of a deep lake. When a stone falls through water it obtains after some time a constant velocity, when the upward friction force from the water plus the upward buoyant force equals the downward gravitational force. When colliding with the bottom sediment layer, the stone penetrates to a certain depth, depending on the properties of the material of the bottom layer. The deformation structure will depend on the geometrical structure and the kinetic energy of the stone, just before it hits the bottom. The Czech researchers have in the laboratory tried to simulate the geometrical and material conditions, being present about 440 million years ago. Tests under these simulated conditions have shown that the deformation depth in the water bottom layer and the geometrical deformation structure are different today from what they were in earlier geological epochs. The most obvious conclusions of these analyses are: Gravity was higher in earlier epochs!
The following papers may be studied:
In the following I shall make some quantitative considerations regarding the differences caused by a decreasing gravity. I shall deduct an equation showing how the acceleration of gravity at the surface of the Earth changes during time, and what changes this gives for bodies falling near the surface of the Earth.
Variation of the acceleration of gravity near the surface of the Earth.According to Newton's 2nd law and Newton's gravitational law, the acceleration of gravity, g, at the surface of the Earth, is given by: (2) 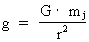 where G is the value of Newton's gravitational 'constant', which varies when the Universe develops, mj is the mass of the Earth and r its radius, which also varies during time. Assuming that mj is constant, we get for the time variation of g, marked with a dot: (3) 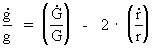 A decreasing G causes a general increase in distance between the gravitating masses. I have earlier shown the validity of the following expansion equation: (4) 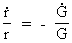 From equations (3) and (4) we get the following context: (5) 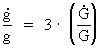 Using the expression from equation (1) we get a context between the relative variation of g and the actual age of the Universe, T: (6) 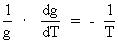 Equation (6) can immediately be integrated: (7) 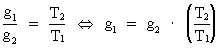 where the indexes 1 and 2 refer to lower and higher ages of the Universe, respectively. The following table shows what the value of g1 has been in earlier epochs of the geological history of the Earth.
The fall of bodies and effects of collisions in different geological epochs.The motions of bodies near to the surface of the Earth are determined by the acceleration of gravity at the chosen place. If gravity were higher in earlier epochs, this will a.o. cause that the velocity of a falling body has been higher, and thereby the kinetic energy. If such body collides with a ground which is deformable, f.i. sand, it will penetrate to a certain depth, and at the same time form a 'collision crater' with a certain geometrical shape, depending on the properties of the material and the kinetic energy, possessed by the body just before the collision. The pressure exerted on the ground will also be determining the crater structure. Everything else equal, a higher acceleration of the body will create a deeper penetration in the ground than a lower acceleration. Let us consider a deep lake with a
deformable bottom layer. Let a stone fall from the surface of the lake
(f.i. melted out of a lump of ice, floating on the surface). Let us assume
that the stone obtains a constant velocity before it reaches the bottom,
and then penetrates this to a depth
(8) 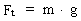 where m is the mass of the stone and g is the actual force of gravity: (9) 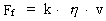
where k is a geometrically
determined factor, (10) 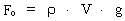
where (11)
The maximum kinetic energy of the stone, Ek,max is given by: (12) 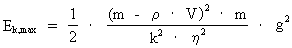
After
the impact with the bottom material, the stone is braked over a distance
(13) 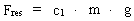 where c1 is a geometrical and material dependent constant.
The depth (14) 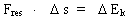
telling us
that the work of the resulting force is equal to the increase in kinetic
energy of a body. Equation (14) is only valid if Fres is
constant over the distance
From equations (12), (13) and (14)
we get for (15) 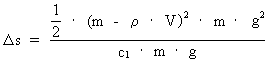 which we, however, shall write as: (16) 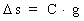 where C is defined by: (17) 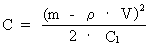
From equation
(16) we see that if C is constant, then (18) 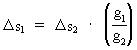 g1 and g2 can be acceleration of gravity at two different ages, corresponding to 'today' and an earlier geological epoch. In places where C has the same value
'today' and in earlier geological epochs,
When calculating the values, I have used that the age of the Universe today is about 10.5 · 109 years, corresponding to the value I have given in my holistic quantum cosmology. A higher value of T2 will not change much in the value for g1 in earlier epochs.
The age of the Universe, determined by paleogravitational studies.Equation (7) gives a context between the accelerations of gravity at the surface of a globe, f.i. the Earth, at two different ages, and this gives a possibility of determining the age of the Universe by paleogravitational analyses. Accurate and confident paleogravitational studies can be helpful in confirming my theory about a continuously decreasing gravity in the Universe. Let us rewrite equation (7) as follows: (19) 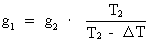
where (20) 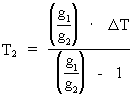
If g2 is the acceleration of gravity at
the surface of the Earth 'today', and g1 and
Louis Nielsen
|
 into the bottom material. We
shall investigate how
into the bottom material. We
shall investigate how 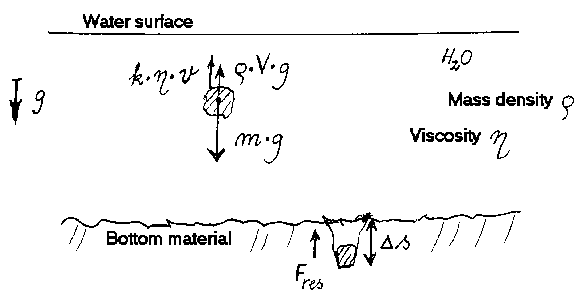
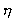 is the viscosity coefficient of the liquid and v is
the immediate velocity of the stone. This velocity is assumed to be fairly
low, so that we can use the first order expression for the friction.
is the viscosity coefficient of the liquid and v is
the immediate velocity of the stone. This velocity is assumed to be fairly
low, so that we can use the first order expression for the friction.
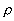 is the mass density of the
liquid and V the volume of
the stone, corresponding to the volume of liquid the stone displaces along
its falling track. After a certain length of this track, the sum of
Ff and Fo will equal Ft, and the maximum
velocity of the stone will have been reached. This maximum velocity
vmax will be given by:
is the mass density of the
liquid and V the volume of
the stone, corresponding to the volume of liquid the stone displaces along
its falling track. After a certain length of this track, the sum of
Ff and Fo will equal Ft, and the maximum
velocity of the stone will have been reached. This maximum velocity
vmax will be given by:
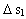 will have
the following values if
will have
the following values if
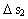 is 10 cm and g2 =
9.82 m/s2.
is 10 cm and g2 =
9.82 m/s2.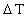 is in million years before 'today'.
is in million years before 'today'.