|
Kvanteenergierne udledt kvantekosmologisk og som konsekvens af rummets, tidens og massens kvantisering Af Louis Nielsen, Herlufsholm Da Max Planck (1858-1947) omkring år 1900 skulle give en forklaring af energifordelingskurven for et energiudstrålende ’absolut sort legeme’, opstillede han en model for de energiudstrålende atomer. Max Planck gjorde følgende ad hoc-antagelser:
Med den sidstnævnte antagelse indførte Max Planck kvantebeskrivelsen af naturfænomenerne. Ifølge den klassiske og matematisk kontinuerte elektromagnetismeteori – som den er udtrykt i de Maxwellske ligninger –, kan et system absorbere og emittere energi i vilkårligt kontinuerte portioner. For den klassisk-mekaniske harmoniske oscillator (dvs. en partikel, der er påvirket af en elastisk kraft) gælder, at den mekaniske energi (dvs. summen af den kinetiske – og elastisk potentielle energi) er proportional med kvadratet på svingningsamplituden. I den kontinuerte klassiske fysik antages denne også at kunne antage alle kontinuerte positive talværdier, i øvrigt uden en øvre maximal værdi. Med Max Plancks kvanteantagelse kan en harmonisk oscillator kun have de diskrete energi-talværdier En givet ved: (1) 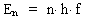 hvor n er et energikvantetal, der kun kan antage talværdierne 1, 2, 3, osv. I den traditionelle bølge-kvantemekanik giver en relativt indviklet
matematisk løsning af Schrödingers kontinuerte bølgeligning
– anvendt på den harmoniske oscillator – de i (1) angivne
energiværdier.
Rationel kvantisering af den harmoniske oscillators mekaniske energi
Det fundamentale grundlag for min ’Holistiske kvantekosmologi’
(se denne) er kvantiseringen af de fysisk fundamentale
størrelser: Afstand, tidsinterval og masse.
(2) 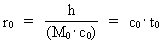 For alle fænomener i vort kvantiserede univers gælder følgende:
(3) 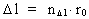 hvor (4) 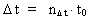 hvor (5) 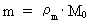 hvor Transformationen fra et klassisk og kontinuert fysikformeludtryk til et kvantefysisk udtryk er blot at indsætte de kvantiserede størrelser givet i (3), (4) og (5). Lad os kvantetransformere formeludtrykket, der angiver den klassisk-mekaniske energi af en harmonisk oscillator. Den mekaniske energi Emek af en harmonisk svingende partikel med massen m og svingningsamplituden A udledes i den klassiske mekanik og er givet ved: (6) 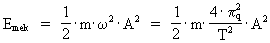 hvor (7) 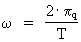 hvor jeg med et indeks q på (8) 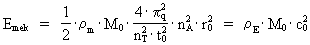 idet c0 = r0/t0 er lysets hastighed.
Ved benyttelse af (2) kan (8) omskrives til: (9) 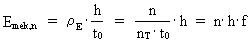 hvor jeg har angivet det rationelle tal Kvantiseret frekvens med øvre og nedre fysiske grænser. Unitonen Som nævnt er udtrykket i (9) matematisk identisk med (1), dog med den store fysiske forskel, at frekvensen i (9) er kvantiseret, hvilket er en konsekvens af tidens kvantisering. I den traditionelle bølgekvantefysik er tidsstørrelsen ikke, og dermed heller ikke en tidsafledt størrelse såsom frekvens, kvantiseret. Ej heller opererer man med fysiske mindste- og størsteværdier af frekvens. Da det fysisk mindste tidsinterval er elementartiden t0, må der til dette høre en fysisk største frekvens fmax givet ved: (10) 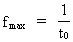 Da det største tidsinterval er universets aktuelle alder Tunivers, må den fysisk mindste frekvens fmin være givet ved: (11) 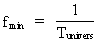 Til den fysisk største frekvens svarer en maximal energi og en hertil ækvivalent maximal masse givet ved: (12) 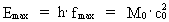 hvor M0 er universets totale masse, og Emax er lig med
den totale energi af hele universet.
(13) 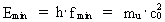
Forening af det mindste med det største Et interessant spørgsmål er: Eksisterer der en sammenhæng mellem de mindste og de største fysiske størrelser i universet? Mit svar er: ja! Begrundelsen for mit svar kan studeres i min 'Holistiske kvantekosmologi', hvor jeg redegør for min opdagelse af følgende sammenhænge: (14) 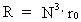 (15) 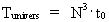 (16) 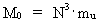
I disse formler spiller N³ rollen som et kosmisk evolutionskvantetal,
der 'tikker' op gennem de naturlige tal. N angiver det aktuelle brøkforhold
mellem de elektrostatiske og gravitostatiske kræfter mellem to elektroner.
Da universet blev 'født', var det kosmiske evolutionskvantetal lig med
én. (17) 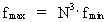 (18) 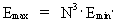 Vi ser, at det kosmiske evolutionskvantetal er den fysiske størrelse, der forener de mindste og de største fysikstørrelser i universet.
© Louis Nielsen, 13. december 1998
|
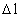 er bestemt ved:
er bestemt ved:
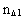 er rumkvantetallet, der kan antage de naturlige talværdier
1, 2, 3, osv.
er rumkvantetallet, der kan antage de naturlige talværdier
1, 2, 3, osv.
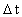 er bestemt ved:
er bestemt ved:
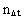 er tidskvantetallet, der kan antage de naturlige talværdier 1, 2, 3, osv.
er tidskvantetallet, der kan antage de naturlige talværdier 1, 2, 3, osv.
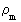 er et rationelt massekvantetal.
er et rationelt massekvantetal.
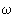 er vinkelhastigheden, der er sammenknyttet med partiklens svingningstid T sådan:
er vinkelhastigheden, der er sammenknyttet med partiklens svingningstid T sådan:
 har angivet,
at man i en fysisk kvantegeometri skal anvende et rationelt pi-tal!
har angivet,
at man i en fysisk kvantegeometri skal anvende et rationelt pi-tal!
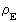 et rationelt energikvantetal. Vi ser meget interessant, at energiindholdet
af en specifik harmonisk oscillator – der er et lokalt subsystem i universet – er
lig med en rationel brøkdel af universets totale energiindhold,
der er bestemt ved M0·c0².
et rationelt energikvantetal. Vi ser meget interessant, at energiindholdet
af en specifik harmonisk oscillator – der er et lokalt subsystem i universet – er
lig med en rationel brøkdel af universets totale energiindhold,
der er bestemt ved M0·c0².